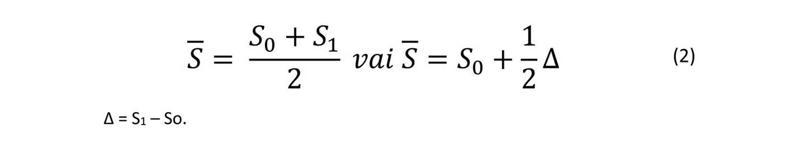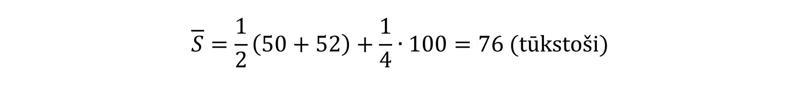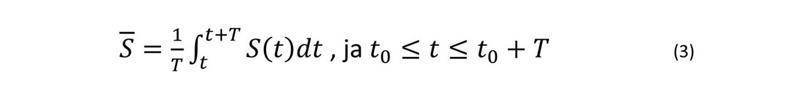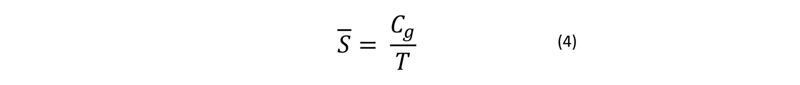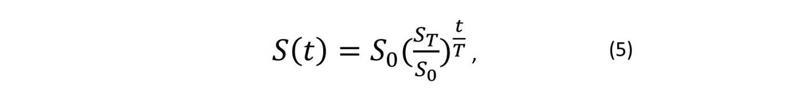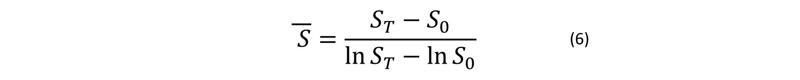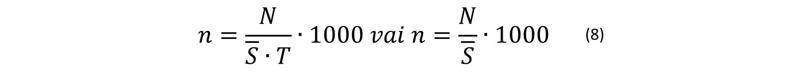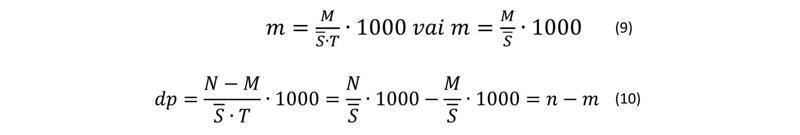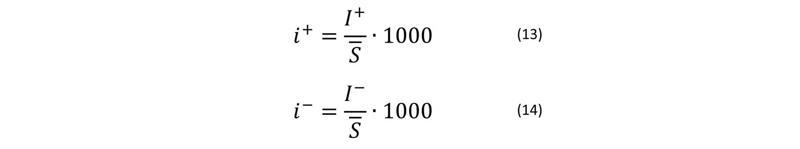Teorētisko un metodoloģisko aspektu aplūkošanā bieži izmanto jēdzienu “vidējie iedzīvotāji”, bet kvantitatīvo rādītāju noteikšanā visbiežāk izmanto vidējo iedzīvotāju skaitu vai atvasinātus vidējos lielumus par iedzīvotāju attīstību.

Vidējo iedzīvotāju apjoms nepārtraukti mainās saistībā ar novērošanas perioda ilgumu (nedēļa, mēnesis, gada ceturksnis, gads, desmitgade un tamlīdzīgi). Šo lielumu parasti aprēķina kā vidējo hronoloģisko. Ja ir ziņas par iedzīvotāju skaitu katrā mēnesī, tad gada vidējo aprēķina pēc šādas formulas:

Ja ir tikai ziņas par iedzīvotāju skaitu gada sākumā un beigās, tad gada vidējo iedzīvotāju skaitu aprēķina kā šo lielumu pussummu.

Šādā gadījumā tiek pieņemts, ka iedzīvotāju skaits gada laikā izmainījies (palielinājies vai samazinājies) vienmērīgi. Ja zināms, ka faktiski tas tā nav bijis, tad aprēķinos jāizdara koriģējumi. Piemēram, ir zināms, ka kādas kūrorta pilsētas klātesošo iedzīvotāju skaits gada sākumā un beigās bija attiecīgi 50 000 un 52 000 cilvēku. Turklāt noskaidrots, ka trīs vasaras mēnešos (t. i., ceturtajā daļā no gada laika fonda) iedzīvotāju skaits vidēji palielinās vēl par 100 000 cilvēku. Vidējo gada klātesošo iedzīvotāju skaitu pilsētā aprēķina šādi:

Arī šī metode vidējo iedzīvotāju aprēķināšanai ir tikai aptuvena, jo faktiski iedzīvotāju skaits dabiskā ceļā un migrācijas dēļ mainās nepārtraukti, arī administratīvi teritoriālo izmaiņu dēļ, un vēlams uztvert visas novērošanas periodā notikušās pārmaiņas. Precīzu rezultātu dod formula, pēc kuras iedzīvotāju skaits dabiskā ceļā un migrācijas dēļ aprēķināms kā funkcija S(t) laika izmaiņām. Tad ir jāiegūst precīzs nodzīvoto cilvēkdienu vai cilvēkgadu skaits, un tas jāizdala ar perioda ilgumu T.

Ja nodzīvoto cilvēkgadu skaitu apzīmē ar Cg, tad vidējā iedzīvotāju skaita formulu var pierakstīt:

Nosacītās (hipotētiskās) paaudzes iedzīvotājiem nodzīvoto cilvēkgadu skaitu Cg parasti iegūst, veidojot mirstības (pārdzīvotības) tabulas. Ilgstošā laika periodā iedzīvotāju skaits nemainās par vienu un to pašu absolūto lielumu. Pareizāks ir pieņēmums, ka izmaiņas notiek kādā pastāvīgā tempā, t. i., ģeometriskā progresijā. Tas nozīmē, ka iedzīvotāju skaits novērošanas periodā mainās šādi:

un vidējais iedzīvotāju skaits aprēķināms pēc formulas:

Piemēram, Ķīnas iedzīvotāju skaits 1964. gadā bija 708,3 miljoni, bet nākamā tautas skaitīšana norisa tikai 1982. gadā. Tajā uzskaitīti 1027,9 miljoni cilvēku. Pēc 6. formulas vidējais iedzīvotāju skaits tautas skaitīšanu starplaikā būs:

Iegūtais iedzīvotāju skaits ir nedaudz mazāks salīdzinājumā ar aprēķinu, kas pamatojas uz vienmērīgu iedzīvotāju absolūtā skaita izmaiņu hipotēzi: 0,5 (708,3 + 1027,9) = 868,1 (miljons).

Ja ir zināms demogrāfisko notikumu skaits periodā un vidējais iedzīvotāju skaits šajā periodā, tad, attiecinot pirmo lielumu pret otro, iegūstami attiecīgo procesu vispārējie raksturotāji, kurus sauc par demogrāfiskiem koeficientiem. Tos demogrāfiskajā analīzē ieviesa 19. gs. sākumā, lai gan idejas par dažāda demogrāfiska satura raksturojumu izteikšanu relatīvo lielumu veidā saistāmas ar angļu zinātnieku Džona Graunta (John Graunt) un Viljama Petija (William Petty) darbību 17. gs.

Dzimstības koeficients (n) iegūstams, attiecinot dzimušo skaitu (N) periodā T (parasti gadā) pret vidējo iedzīvotāju skaitu šajā pašā laikā.

Bieži vien šo un citu tāda tipa formulu pierakstos reizinājumu ar 1000 izlaiž. Analoģiskas formulas iegūstam arī mirstības (m) un dabiskā pieauguma (dp) raksturošanai.

Attiecības N/T un M/T ir dzimšanas un miršanas gadījumu skaits laika vienībā. Dažkārt tās dēvē par dzimšanas un miršanas blīvumiem (biežumiem).

Laulību noslēgšanas jeb laulātības (l) un laulību šķiršanas (š) koeficientus aprēķina, izmantojot šādas formulas:

Ar līdzīgiem koeficientiem raksturo arī iedzīvotāju migrāciju. Ja ar I⁺ apzīmē kādā valstī (apdzīvotā vietā) imigrējušo (iebraukušo) un ar I^- emigrējušo (izbraukušo) iedzīvotāju skaitu, tad, attiecinot tos pret vidējo iedzīvotāju skaitu, iegūst attiecīgos migrāciju raksturojošos relatīvos rādītājus – koeficientus i⁺ un i^-:

Šo divu relatīvo rādītāju starpība raksturos iedzīvotāju migrācijas saldo (pieauguma vai samazinājuma) līmeni (mp).

Lai pētītu iedzīvotāju attīstību, īpaši demogrāfisko procesu intensitāti, nepieciešams aplūkot attiecīgos raksturlielumus atsevišķi sievietēm un vīriešiem un arī specifiskām to vecumu grupām, nevis tikai visā iedzīvotāju kopumā vidēji. Piemēram, dzimstības pētījumos ļoti svarīgi izmantot rādītājus reproduktīvā vecuma sievietēm, bet migrācijas pētījumos parasti interesējas par jaunākā un vidējā vecuma darbspējīgajiem iedzīvotājiem. Katram vecumam aprēķinātie demogrāfisko procesu intensitātes secīgie rādītāji un atsavinātie demogrāfisko notikumu iestāšanās varbūtības lielumi veido demogrāfisko tabulu saturu. To veidošanas gaitā iegūst arī attiecīgo procesu raksturojošus rezultējošos rādītājus: vidējo dzimušo bērnu skaitu noteiktu kohortu sievietēm, vidējo mūža ilgumu vīriešiem un sievietēm, vidējo vecumu līgavām un līgavaiņiem, visiem dzīvojošiem (laikabiedriem) un tamlīdzīgi. Nereti vidējo iedzīvotāju skaitu izmanto izglītības, veselības aprūpes, sociālās nodrošināšanas un citās nozarēs. Tipiski ir ekonomiska rakstura aprēķini par iekšzemes kopproduktu uz vienu cilvēku vai vienu nodarbināto, pārtikas un nepārtikas preču patēriņu, vidējo apdzīvojamo platību ģimenei vai mājsaimniecībai. Daudzās sociālās statistikas jomās plaši lieto ne vien pakāpju vidējos, bet arī struktūras vidējos: modu – varianti, kurai sadalījuma rindā ir vislielākais svars (biežums) –, mediānu (ranžētas sadalījuma rindas vidū esošās vienības), kvartiles, kvintiles un citus. Izteiktāk tas vērojams demogrāfisko procesu diferenciācijas, mājsaimniecību sastāva, ienākumu un sociālās nevienlīdzības izpētē. Piemēram, saskaņā ar ranžēto valstu sadalījumu pēc iedzīvotāju vecuma visaugstākā mediānas vērtība sistemātiski tiek fiksēta Monako (53,1 gads 2018. gadā), Japānā (47,3) un Vācijā (47,1), bet visjaunākie ir Nigēras (15,4 gadi) un Ugandas (15,8) iedzīvotāji.