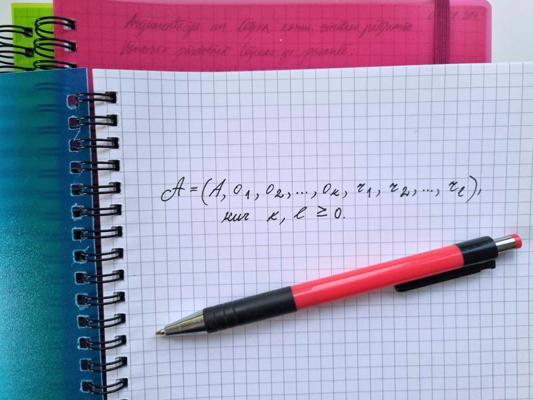Pirmsākumos algebrā nodarbojās ar parastajām skaitliskajām operācijām (darbībām), piemēram, saskaitīšanu vai reizināšanu, un abstraktā algebra kopš savas rašanās daudzus gadu desmitus ir tikusi raksturota kā matemātikas nozare, kas saistīta ar patvaļīgās kopās definētām patvaļīgām operācijām un šādu struktūru īpašībām. Līdz ar to arī apzīmētājs “algebrisks” daudzos gadījumos ir nozīmējis saistību ar operācijām, arī nosaukumos “algebriska sistēma”, “algebriska struktūra”. Lielākā daļa algebras praksē sastopamo algebrisko sistēmu tiešām ir kopas ar operācijām un bez attiecībām, taču ne visas. Piemēram, sakārtotā grupā vai gredzenā blakus operācijām tiek aplūkota arī t. s. sakārtojuma attiecība, bet režģi var ekvivalenti definēt gan kā kopu ar divām operācijām, gan kā kopu ar vienu attiecību (kuras pakļaujas attiecīgām aksiomām). Mūsdienās algebra pievēršas arī patvaļīgām sistēmām ar operācijām un attiecībām (retāk sistēmām, kurās ir tikai attiecības), tomēr minētais vārda “algebrisks” lietojums ir daudzviet saglabājies (blakus vēl citām tā nozīmēm).

Turpmāk ir skatītas algebriskas sistēmas plašākajā nozīmē, aprobežojoties ar izplatītāko vienas kopas gadījumu. Algebrisku sistēmu, kurā ir tikai operācijas, sauc par “algebru” (nejaukt ar t. s. algebru pār lauku, kas ir īpaša veida sistēma, un ar algebru kā nozari), bet tādu, kur uzdotas tikai attiecības – par “modeli” (arī šim terminam ir vairākas nozīmes) vai “relacionālu sistēmu” (un tad pretstatam ar algebrisku sistēmu nereti saprot sistēmu bez attiecībām, t. i., algebru). Dažkārt sistēmā blakus operācijām un attiecībām uzrāda arī kādus īpašus kopas elementus, t. s. konstantes; šādu gadījumu var īpaši neizdalīt, ja elementus uzskata par 0-vietīgām jeb bezargumentu operācijām. Noteiktiem mērķiem (piemēram, matemātiskajā loģikā) var būt lietderīgi attiecību vietā lietot predikātus.

Termins “algebriska sistēma” 20. gs. 60. un 70. gadu mijā padomju algebras skolas iespaidā pārņemts no krievu valodas. Daudzās valodās algebrisko sistēmu parastais nosaukums ir “struktūra” (angļu structure, vācu Struktur, franču structure) vajadzības gadījumā ar kādu precizējošu apzīmētāju (bieži – pirmās pakāpes struktūra), bet nosaukumu “algebriska sistēma” tur vairāk lieto kā īsinājumu terminam “algebrisku vienādojumu sistēma”. Šajā tradīcijā algebras sauc arī par “algebriskām struktūrām”, bet modeļus – “par relacionālām struktūrām”. Taču arī te sastopamas variācijas; piemēram, nereti par algebrisku (vai relacionālu) struktūru kādā kopā sauc tur uzdotu operāciju (respektīvi, attiecību) kopumu, dažkārt līdz ar norādītām aksiomām, kas operācijām (attiecībām) jāapmierina, citkārt arī bez tām. Piemēram, kad saka, ka kopā uzdota gredzena struktūra, tas nozīmē, ka norādītas tur definētas operācijas, kas apmierina gredzena aksiomas; tad var teikt, ka gredzens ir kopa, kurā uzdota gredzena struktūra. 

Pastāv vairāki veidi, kā algebriskas sistēmas jēdzienu mēdz formāli definēt; tie atšķiras ar to, kā “uzdod” sistēmas operācijas un attiecības. Šeit pieņemtais ir nosacīti vienkāršākais un ir parocīgs, runājot par atsevišķām sistēmām, taču nepietiekams, kad, piemēram, jārunā par aksiomātiski aprakstāmām algebrisko sistēmu klasēm. Tad sistēmas aprakstā iesaista t. s. signatūru.

Vispārīgā gadījumā algebriska sistēma 𝒜 ∶= (𝐴, 𝑂, 𝑅) ir netukša kopa 𝐴, aplūkota kopā ar tajā definētu operāciju saimi 𝑂 := (𝑜_𝑖 : 𝑖 ∈ 𝐼) un attiecību saimi 𝑅 ∶= (𝑟_𝑗 : 𝑗 ∈ 𝐽). Katra no šīm saimēm var būt galīga, bezgalīga vai pat tukša. Kopu 𝐴 sauc par sistēmas 𝒜 pamatkopu, arī par domēnu vai tās (precīzāk, tās operāciju un attiecību) nesējkopu. Operācijas no 𝑂 sauc par sistēmas 𝒜 galvenajām jeb pamatoperācijām, attiecības no 𝑅 – par tās galvenajām jeb pamatattiecībām, bet tās operācijas un attiecības, kas ar šo palīdzību var tikt kopā 𝐴 definētas, – par atvasinātām. Divas sistēmas uzskata par vienādām, ja tām ir kopēja pamatkopa un sakrīt to pamatoperāciju un arī to pamatattiecību saimes. Ja sistēma 𝒜 ir algebra (t. i., saime 𝑅 ir tukša), to pieraksta vienkāršāk kā pāri (𝐴, 𝑂); līdzīgi, ja 𝒜 ir modelis (tukša ir saime 𝑂). Īpašā gadījumā, kad tukšas abas saimes, sistēma ir vienkārši kopa bez norādītas iekšējas struktūras. Visbiežāk abas saimes 𝑂 un 𝑅 ir galīgas virknes, kurās operācijas, respektīvi, attiecības indeksētas ar naturāliem skaitļiem; tālāk pieņemta tieši šī noruna. Tātad

𝒜 = (𝐴, 𝑜₁, 𝑜₂, ... , 𝑜_𝑘, 𝑟₁, 𝑟₂, ... , 𝑟_𝑙), kur 𝑘, 𝑙 ≥ 0.

Katrai sistēmas 𝒜 pamatoperācijai 𝑜_𝑖 un katrai pamatattiecībai 𝑟_𝑗 ir savs noteikts argumentu vietu skaits jeb t. s. aritāte 𝛼_𝑖, respektīvi, 𝛽_𝑗. Pāri 𝜏 ≔ (𝛼; 𝛽), kur 𝛼 ir virkne ∝₁, ∝₂, ... , ∝_𝑘, bet 𝛽 ir virkne 𝛽₁, 𝛽₂, ... , 𝛽_𝑙, sauc par sistēmas 𝒜 līdzības tipu vai vienkārši tipu; algebrai tās tips ir vienkārši (𝛼), modelim – (𝛽). Algebriskas sistēmas, kurām ir viens līdzības tips, sauc par līdzīgām. Par divu līdzīgu sistēmu pamatoperācijām 𝑜_𝑖 un 𝑜^′_𝑖, kurām ir vienādi indeksi, tātad arī vienāds argumentu skaits, saka, ka tās ir viena otrai atbilstošas jeb viena nosaukuma operācijas, un tāpat raksturo abu sistēmu atbilstošās jeb viena nosaukuma attiecības.

Tādējādi – visu to algebrisko sistēmu klasi, kas līdzīga kādai dotai sistēmai, pilnībā nosaka šīs sistēmas līdzības tips. Mēdz rīkoties arī otrādi: izvēlas abstraktu tipu 𝜏 ∶= (𝛼; 𝛽), kur 𝛼 un 𝛽 ir kādas nenegatīvu veselu skaitļu saimes, un aplūko visu to algebrisko sistēmu klasi 𝒜(𝜏), kuru līdzības tips ir 𝜏.

Algebras (ℤ, +,×) un (ℤ,×, +), kur ℤ ir veselo skaitļu kopa, bet + un × – parastās operācijas, ir līdzīgas, taču dažādas (2,2) tipa algebras (jeb (2,2;) tipa algebriskas sistēmas). Unāra algebra ir kopa ar vienu vienvietīgu operāciju, t. i., jebkura (1) tipa algebra (virknē 𝛼 ir viens loceklis 1). Grupa multiplikatīvā pierakstā ir algebra (𝐴,∙,⁻¹ , 𝑒) ar reizināšanu, apgrieztā elementa ņemšanu ⁻¹ un neitrālo elementu e, tās tips ir (2,1,0). Sakārtota grupa ir (2,1,0;2) tipa algebriska sistēma (𝐴,∙,⁻¹ , 𝑒, ≤), kur ≤ ir sakārtojuma attiecība kopā 𝐴. Modeļu piemēri ir reālo skaitļu kopa (ℝ, <) ar parasto attiecību “mazāks par” (tā tips ir (1)) un plaknes taišņu kopa (𝑇, ∥, ⊥) ar attiecībām “paralēls” un “perpendikulārs” (tips (2,2)).

Operācijas un attiecības algebriskā sistēmā parasti pēc noklusējuma tiek domātas ar galīgu argumentu vietu skaitu, visur pamatkopā definētas un vienvērtīgas, tomēr ir arī svarīgi izņēmumi. Piemēram, pilns režģis ir piemērs infinitārai algebrai – algebrai ar operācijām, kam ir bezgalīgi daudz argumentu (argumentu vietu). Savukārt, veselo skaitļu gredzenā dalīšanu, tātad arī dalāmības attiecību var definēt tikai daļēji, bet lauks pēc definīcijas ir sistēma, kurā pamatoperācija apgriešana nav definēta nullei. Algebriskas sistēmas, kur starp pamatoperācijām vai pamatattiecībām ir daļēji definētas, arī sauc par daļējām. Multialgebras ir algebru vispārinājums, kur pieļauj vairākvērtīgas operācijas (piemēram, kvadrātsaknes operācija komplekso skaitļu laukā), tādas sistēmas sastopamas retāk.

Vairāksugu (saka arī vairākšķiru; angļu many-sorted, vācu vielsortige, heterogene, franču hétérogène, krievu многосортная) algebriska sistēma rodas, kad ir vairākas kopas ar dažādu veidu (“sugu”) elementiem un aplūko tajās definētas operācijas vai attiecības. Šādā sistēmā divu vai vairāku argumentu operācijai vai attiecībai tās argumenti var būt no dažādām kopām, tāpat jebkura no kopām var būt operācijas vērtību kopa. Vienkāršs divsugu algebras piemērs ir jebkura vektoru telpa. Tā sastāv no vektoru kopas un skalāru kopas; divus vektorus var saskaitīt, vektoru var reizināt ar skalāru, iegūstot atkal vektoru, bet skalāri visbiežāk ir reālie skaitļi ar to parastajām operācijām. Vektora reizināšana ar skalāru te ir jaukta tipa divu argumentu operācija.

Lietojumos algebriskas sistēmas ir noderīgs līdzeklis kādu strukturētu objektu vai situāciju (noteiktu to aspektu) aprakstīšanai, lai varētu tos raksturot un izpētīt ar algebriskām metodēm. Taču, neatkarīgi no savas izcelsmes, tiek pētītas arī pašas algebriskās sistēmas. Gan atsevišķas interesantas sistēmas, gan savā starpā radniecīgu sistēmu kopīgās īpašības pētī abstraktajā algebrā, bet pašas šādu sistēmu klases pētī tās apakšvirzienā – vispārīgajā algebrā. Starp svarīgākajiem ar algebriskajām sistēmām saistītajiem objektiem un konstrukcijām, par ko abstraktā algebra interesējas, ir: algebrisko sistēmu kongruences, ideāli, endomorfismi; to apakšsistēmas un faktorsistēmas; to reducēšana un izvēršana; to Dekarta un citādi reizinājumi; homomorfismi starp sistēmām.

Atsevišķas algebriskas sistēmas faktiski bija pazīstamas jau senatnē. To pamatā bija konkrētas skaitļu (naturālo, vēlāk arī veselo un reālo) kopas kopā ar parastajām aritmētiskajām darbībām un ar parastajām salīdzināšanas (lielāks par u. tml.) attiecībām. Taču nebija vajadzības pēc vispārīga algebriskas sistēmas jēdziena. Tāda vajadzība radās tikai 19. gs., kad ievēroja, ka noderīgas un pietiekami interesantas darbības jeb operācijas var izpildīt ne vien ar skaitļiem, bet arī ar citiem matemātiskiem (un ne tikai) objektiem. Turklāt vairākas šo jauno operāciju īpašības ir līdzīgas saskaitīšanas un reizināšanas īpašībām. Pirmie nozīmīgie tādu neskaitlisku algebru piemēri parādījās 1832. gadā, kad Evarists Galuā (Évariste Galois), pētot polinomiālo vienādojumu atrisināmību, atklāja tā dēvētās simetriju grupas; arī lauku un sakārtoto lauku izcelsme saistāma ar šo pašu problemātiku. Lai gan grupas un lauka idejas var saskatīt Kārļa Frīdriha Gausa (Johann Carl Friedrich Gauß), Žozefa Lagranža (Joseph-Louis Lagrange) un Ogista Košī (Augustin Lois Cauchy) pētījumos jau iepriekšējā gadsimtā, abstrakta grupas definīcija gan tika ieviesta tikai 1854. gadā, bet lauka definīcija – 1893. gadā. Tomēr pats “sistēmu formēšanas” process bija sācies, radās arī citas algebriskas sistēmas (Būla algebra klašu loģikā, matricu un kvaternionu algebras u. c.), un kopumā tas noveda pie nozīmīga notikuma algebras vēsturē – abstraktās algebras (tolaik saukta arī par moderno) rašanās. 

Matemātikas, tai tuvāko dabaszinātņu, arī datorzinātņu attīstība ir novedusi pie daudzu dažāda veida algebrisku sistēmu atklāšanas arī 20. gs., piemēram, režģu, Hopfa, relāciju, procesu, operatoru, BCK algebras, ortomodulāras sakārtotas kopas un to vispārinājumi. Gareta Birkhofa (Garret Birkhoff) 20. gs. 30. gadu publikācijas aizsāka laika posmu, kad algebristi pievērsās jautājumiem, kas kopīgi dažādām algebriskām sistēmām. 20. gs. 40. gados un vēlāk ievērojamu ieguldījumu algebriskas struktūras jēdziena veidošanā un formalizēšanā, kā arī dažādu algebrisku sistēmu teorijas izveidošanā deva franču matemātiķu grupa ar kolektīvu pseidonīmu Nikolā Burbaki (Nicolas Bourbaki). Gadsimta otrajā pusē jau bija izveidojusies vispārīgā jeb universālā algebra – vispārīga algebrisko sistēmu, pirmām kārtām, algebru, teorija (Alfrēds Tarskis (Alfred Tarski (arī Alfred Tajtelbaum), Anatolijs Maļcevs (Анатолий Иванович Мальцев) un citi).