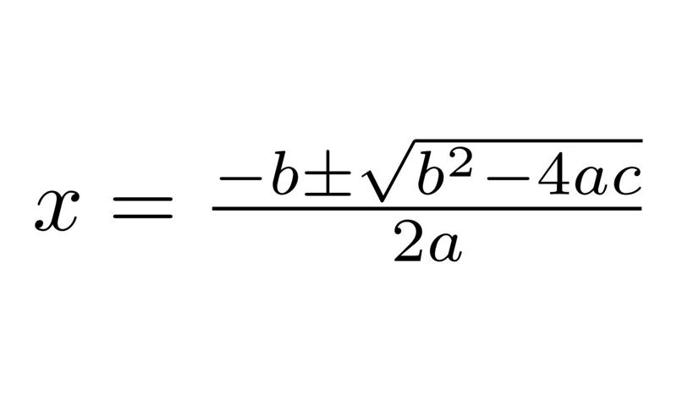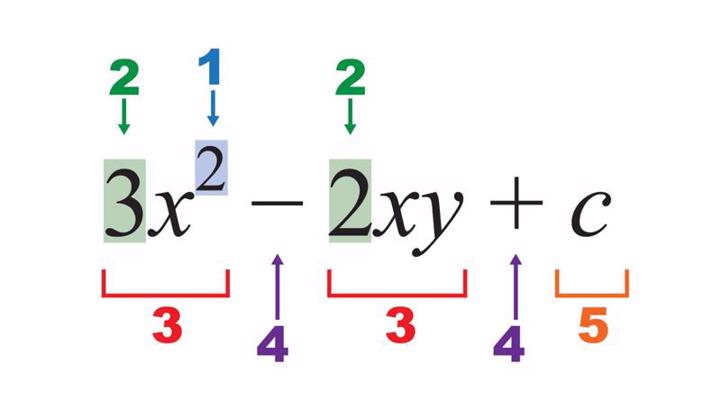Algebras saturs laika gaitā mainījies no skaitlisku vienādojumu pārveidošanas un risināšanas mākslas senatnē līdz vispārīgai algebrisku sistēmu teorijai. Tā radusies no centieniem atrast un izskaidrot vispārīgus paņēmienus dažādu veidu aritmētikas uzdevumu risināšanai, kur jāizpilda darbības ar skaitliskiem lielumiem vai tie jāsalīdzina. Kad lielumus sāka apzīmēt ar burtiem, radās iespēja aprakstīt un pētīt pašu darbību īpašības, kā arī izteikt uzdevumu saturu ar vienādojumiem un vienādojumu sistēmām, arī ar vairākiem nezināmajiem. Šādu vienādojumu un to sistēmu pētīšana, kā arī atrisināšanas paņēmienu noskaidrošana ilgus gadsimtus bija algebras galvenais saturs. Pamazām radās izpratne, ka aritmētiskajām, tas ir, skaitliskām, līdzīgas darbības jeb operācijas var izpildīt arī ar citādas dabas matemātiskiem objektiem (matricām, polinomiem, kopām u. c.); dabaszinātņu un tehnikas attīstība radīja arī praktisku nepieciešamību lietot un izprast operācijas dažādās objektu kopās, tāpat arī tā izveidojošos algebrisku sistēmu vispārīgas īpašības. Tāpēc algebra tagad kļuvusi par pamatā abstraktu zinātni, kas tādējādi var tikt un tiek izmantota ne vien citās zinātnes nozarēs, bet joprojām arī jaunu, praktisku uzdevumu risināšanā. Algebra kā termins matemātikas nozares apzīmēšanai fiksēts 16. gs. Mūsdienās vārds “algebra” tiek lietots arī šaurākās nozīmēs: tā sauc patvaļīgu kopu ar tajā uzdotām jebkādām operācijām (darbībām) jebkādā skaitā (saka arī – universāla algebra, abstrakta algebra); bet tas var nozīmēt arī īpaša veida šādu algebru, respektīvi – t. s. algebru pār lauku (vai gredzenu). Kopā ar apzīmētāju to izmanto dažu algebras apakšnozaru nosaukumos, piemēram, lineārā algebra, elementārā algebra, kā arī dažu abstraktu algebru vai to klašu nosaukumos, piemēram, kopu algebra, Būla algebra, Banaha algebra, sakārtota algebra. Arī atvasinātais nosaukums var būt daudznozīmīgs, piemēram, visu Būla algebru teoriju arī sauc par Būla algebru.
algebra
Saistītie šķirkļi
Algebras vienādojumi. 2009. gads.
Algebrā tradicionāli izšķir trīs vēsturiski veidojušās konceptuālas sastāvdaļas: elementāro algebru, abstrakto algebru un universālo algebru; visi šie virzieni joprojām attīstās. Elementārā algebra izmanto pašus vienkāršākos pamatjēdzienus, kas saistīti ar reālajiem (arī kompleksajiem) skaitļiem un darbībām ar tiem. Elementārās algebras iezīmes atrodamas jau agrīno viduslaiku matemātikā, bet tā izveidojusies no 16. gs. līdz 19. gs. pirmajai pusei. Algebra, kuru māca skolās, ir elementārā algebra; tās darbības lauks ir reālo vai komplekso skaitļu sistēma. Abstraktā (jeb modernā vai mūsdienu) algebra apskata dažādas radniecīgu algebrisku sistēmu klases, ko apraksta ar aksiomām. Iegūtie rezultāti (apgalvojumi, konstrukcijas, metodes) var tikt attiecināti uz atsevišķām attiecīgās klases algebrām, tā izvairoties no vajadzības iegūt rezultātu atkārtoti konkrētām sistēmām. Vēsturiski pirmās un pazīstamākās ir grupas un skaitļu sistēmu vispārinājumi – gredzeni un lauki. Veidojusies kopš 19. gs. vidus; tās attīstība pamatā notiek, rodoties jauniem, katrai algebrisko sistēmu klasei raksturīgiem uzdevumiem. Abstraktās algebras apakšnozares ir augstskolu algebras kursu pamatā. Universālā (jeb vispārīgā) algebra ir virziens un posms abstraktajā algebrā. Tā koncentrējas uz visu vai arī tai vai citai plašai algebru klasei piederošo algebrisko sistēmu kopējām īpašībām, neinteresējoties par konkrētām aksiomām, proti, ieved jēdzienus, kas vienlīdz piemērojami režģiem, grupām, gredzeniem u. c., atrod visām apskatāmajām sistēmām kopīgas iezīmes un pierāda tām visām derīgus apgalvojumus. Šis virziens sācis veidoties 20. gs. 30.–40. gados.
Mūsdienu algebras abstraktās būtības dēļ no 20. gs. vidus vērojama matemātikas un citu zinātņu algebrizācija – to uzdevumu pārtulkošana algebras valodā un algebras daudzveidīgo matemātisko līdzekļu izmantošana. Elementārā algebra ir ceļvedis algebrisku vienādojumu un vienādojumu sistēmu risināšanā gan ikdienas praksē, gan dažādās zinātņu nozarēs. Abstraktās algebras jēdzieni, metodes, teorijas tiek izmantotas arī citās matemātikas apakšnozarēs, piemēram, algebriskajā skaitļu teorijā, ģeometrijā, loģikā, diferenciālvienādojumu teorijā un ārpus matemātikas, piemēram, ekonomikā (lineārā algebra, lineārā un nelineārā programmēšana), kvantu mehānikā (galīgo grupu reprezentācijas teorija, operatoru algebras), datorzinātnē (algebriskas sistēmas datu teorijā), kristalogrāfijā un citur, kur tiek pētītas simetrijas (grupu teorija). Universālās algebras, tai skaitā kategoriju teorijas, metodes lieto matemātiskajā loģikā, fizikas, īpaši kvantu mehānikas, modeļu un konceptuālo struktūru raksturošanai, arī teorētiskajās datorzinātnēs.
Matemātikas tematu klasifikācijas shēmā (Mathematics Subject Classification, MSC, 2010) matemātika ir iedalīta vairākās nozarēs. No tām uz algebru attiecas sakārtojumi, režģi un sakārtotas algebriskas struktūras; vispārīgas algebriskas sistēmas; skaitļu teorija (daļēji); lauku teorija un polinomi; komutatīvā algebra; algebriskā ģeometrija (daļēji); lineārā un multilineārā algebra ar matricu teoriju; asociatīvie gredzeni un algebras; neasociatīvie gredzeni un algebras; kategoriju teorija un homoloģiskā algebra; K teorija; grupu teorija un tās vispārinājumi; topoloģiskās (daļēji) un Lī grupas. Katrā no šīm apakšnozarēm klasifikācijas shēmā iezīmēti vairāki apakšvirzieni, kas katrs iedalīti vēl sīkāk. Vērtējot algebras apakšnozares un radniecīgu apakšnozaru grupas pēc publikāciju skaita un tātad tajās strādājošu algebristu skaita, svarīgākās ir skaitļu teorija, grupu teorija ar vispārinājumiem un gredzenu, lauku un algebru teorija. Mazāk darbu ir lineārajā un multilineārajā algebrā, vēl mazāk - pārējās apakšnozarēs.
Algebras sākotne meklējama ap 2000. gadu vidu p. m. ē., kad jau pazina naturālos skaitļus un parastās aritmētiskās darbības. Ēģiptiešu priesteri risināja pirmās pakāpes un arī vienkāršākus otrās pakāpes vienādojumus. Babilonijas matemātiķi prata atrast pozitīvās saknes kvadrātvienādojumiem ar pozitīviem koeficientiem, negatīvie skaitļi vēl nebija pazīstami. Arī Ķīnā tajā laikā prata risināt lineāros un kvadrātvienādojumus, risināja arī vienādojumu sistēmas ar vairākiem nezināmajiem un izmantoja negatīvus skaitļus. Jo īpaši strauja matemātikas attīstība sākās 4. gs. p. m. ē. Grieķijā. Lielākie grieķu algebras sasniegumi ir saistīti ar 3. gs. dzīvojušo Diofantu no Aleksandrijas (Διόφαντος ὁ Ἀλεξανδρεύς), kurš deva ieguldījumu ne vien vienādojumu, bet arī (mūsdienu terminoloģijā) skaitļu teorijā un algebriskajā ģeometrijā. Diofanta grāmatu sērija “Aritmētika” (Ἀριθμητικά) ir grieķu matemātikas ievērojamākais darbs papildus Eiklīda (Εὐκλείδης) “Elementiem” (Στοιχεῖα). Nākamais nozīmīgais algebras attīstības posms 7.–15. gs. saistās ar Indiju un islāma zemēm. Ap 825. gadu persiešu matemātiķis un astronoms Muhameds bin Mūsā al Horezmī (محمد بن موسى خوارزمی) uzrakstīja populārzinātnisku grāmatu “Īsa grāmata par rēķiniem ar atjaunošanu un izlīdzināšanu” (arābu الكتاب المختصر في حساب الجبر والمقابلة, Al-kitāb al-mukhtaṣar fī ḥisāb al-ğabr wa’l-muqābala; latīņu Liber Algebræ et Almucabola). Uzskata, ka tās nosaukumā vārds al-ğabr ‘atjaunošana’ mūsdienu valodā nozīmē mazinātāja pārnešanu no vienādojuma vienas puses uz otru par saskaitāmo, bet wa’l-muqābala – vienādu locekļu saīsināšanu tā abās pusēs (eksistē arī citi viedokļi gan par abu vārdu tulkojumiem, gan jēgas izskaidrojumu). Grāmatā ar rēķiniem ir saprasta galvenokārt kvadrātvienādojumu atrisināšana pozitīvos skaitļos, kas pirmo reizi arī pilnībā izskaidrota. Šī grāmata pārveidoja toreizējo algebru (proti, zemāko pakāpju vienādojumu teoriju). Tā kļuva par vienojošu teoriju, kas iekļāva arī racionālos un iracionālos skaitļus un ģeometriskos lielumus, traktējot tos visus kā viena veida objektus. Šādas algebriskas domāšanas parādīšanās veicināja algebras plašu perspektīvu nākotnē. Pēc matemātikas attīstības apsīkuma agrīnajos viduslaikos algebra savu atdzimšanu Eiropā piedzīvoja, kad tur kļuva zināmi arābu avoti (tostarp minētā al Horezmī grāmata) un jau aizmirsto senās Grieķijas autoru, tostarp Diofanta, darbi, kurus 12. gs. sāka tulkot latīniski. 15. gs. sākās matemātikas noriets islāma pasaulē, bet tās attīstības centrs pārvietojās uz renesansi piedzīvojušo Eiropu. Pagrieziena punkts algebras vēsturē ir franču matemātiķa Fransuā Vjeta (François Viète) izveidotā simbolu lietošanas sistēma 16. gs. otrā pusē. Tā ļāva kompakti pierakstīt vienādojumus, aprakstīt aritmētikas likumus un rēķināšanas algoritmus, kā arī dot tam algebrisku pamatojumu. Šī sistēma gan vēl nebija līdzīga mūsdienās pierastajai un bija visai smagnēja. Mūsdienu simbolu sistēmu ieviesa franču filozofs un matemātiķis Renē Dekarts (René Descartes) 1637. gadā publicētajā grāmatā “Ģeometrija” (La Géométrie), liekot pamatu arī analītiskajai ģeometrijai. 16. gs. algebriski tika vispārīgā veidā atrisināti trešās un ceturtās pakāpes vienādojumi un pamatotas to sakņu aprēķināšanas formulas (mūsdienās pazīstamas kā Kardano formulas). Tikai 19. gs. sākumā izdevās pierādīt, ka vispārīgā veidā piektās un augstāku pakāpju vienādojumus ar algebriskām metodēm atrisināt nav iespējams. Tomēr veiktais darbs kopā ar moderno algebras simboliku bija veicinājuši polinomu algebras attīstību. Savukārt lineāro vienādojumu sistēmu risināšanas vajadzībām tika izdomātas matricas un determinanti; ar šo aizsākās lineārā algebra. 19. gs. laikā algebra piedzīvoja strauju attīstību. Notika arī ievērojamas kvalitatīvas izmaiņas, kuru rezultātā gan algebras saturs, galvenās idejas un metodes, gan tās vieta un loma matemātikā krasi mainījās. Īpaši attīstījās trīs galvenie pētījumu virzieni, no kuriem izveidojās abstraktā algebra: algebriskā skaitļu teorija (vācu matemātiķi: Kārlis Frīdrihs Gauss (Johann Carl Friedrich Gauß), Rihards Dedekinds (Julius Wilhelm Richard Dedekind), Leopolds Kronekers (Leopold Kronecker)), permutāciju un ģeometrisko transformāciju grupu teorija (franču matemātiķi: Evarists Galuā (Évariste Galois), Edmons Žordāns (Marie Ennemond Camille Jordan), norvēģu matemātiķis Nilss Henriks Ābels (Niels Henrik Abel)), lineārā algebra un hiperkompleksie skaitļi (vācu matemātiķis Hermans Grasmans (Hermann Günter Grassmann), britu un amerikāņu matemātiķis Džeimss Džozefs Silvesters (James Joseph Silvester), britu matemātiķis Arturs Keilijs (arī – Arturs Keli) (Arthur Cayley).
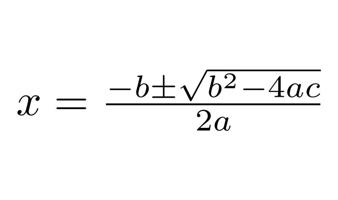
Kvadrātiskā formula izsaka kvadrātvienādojuma ax2 + bx + c = 0 (kur a nav 0) saknes ar tā koeficientiem.
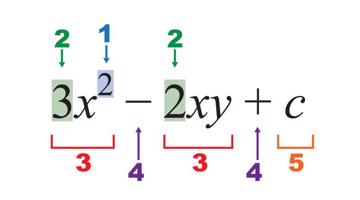
Algebrisku izteiksmju pieraksts: 1 – kāpinātājs, 2 – koeficients, 3 – loceklis, 4 – operācijas simbols, 5 – brīvais loceklis, x,y – mainīgie, c – konstante.

Muhameda bin Mūsā al Horezmī piemineklis Hivā. Uzbekistāna, 22.09.2014.

Fransuā Vjets. 1861. gads.

Renē Dekarts. 19. gs.
20. gs. otrajā pusē, attīstoties skaitļošanas tehnikai, radās pieprasījums pēc skaitlisko metožu attīstības lineārajā algebrā un dažās citās apakšnozarēs. Ir nepieciešami jau pazīstamo aprēķinu metožu sarežģītības, piemēram, laikietilpības novērtējumi, un tiek izstrādātas arī jaunas. Teorētiskā plāksnē vērojama intereses pārbīde no komutatīvām uz nekomutatīvām (galvenokārt fizikas vajadzībām) un no daudzdimensiju uz bezgalīga skaita dimensiju algebriskajām struktūrām. Savu vietu nezaudē grupu teorija, straujāk attīstās Lī grupu teorija, homoloģiju teorija, K teorija.
Nozīmīgākie algebras periodiskie izdevumi: Algebra Colloquium (kopš 1994. gada; World Scientific); Алгебра и логика (kopš 1962. gada; Сибирский фонд алгебры и логики), Algebra Universalis (kopš 1971. gada; Springer); Communications in Algebra (kopš 1974. gada; Taylor & Francis); Journal of Algebra (kopš 1964. gada; Elsevier (Academic Press)); Journal of Group Theory (kopš 1998. gada; De Gruyter); Journal of Pure and Applied Algebra (kopš 1991. gada; Elsevier (North-Holland)); Linear and Multilinear Algebra (kopš 1973. gada; Taylor & Francis); Semigroup Forum (kopš 1970. gada; Springer).
Ievērojami pētnieciskie centri, kas guvuši nozīmīgu starptautiska mēroga atzinību, ir: Bernes Universitātes Matemātikas institūts (Institute of Mathematics, University of Bern) Šveicē, Krievijas Zinātņu akadēmijas Sibīrijas nodaļas S. L. Soboļeva Matemātikas institūts (Институт математики имени С. Л. Соболева Сибирского отделения Российской академии наук (saīsināti – ИМ СО РАН))Novosibirskā, Krievijā, Oksfordas Universitātes Matemātikas institūts (The Mathematical Institute, University of Oxford) Lielbritānijā, Vanderbiltas Universitātes Matemātikas nodaļa (Department of Mathematics, Vanderbilt University) Nešvilā, ASV, Krievijas Zinātņu akadēmijas V. A. Steklova Matemātikas institūta Sanktpēterburgas nodaļa (Санкт-Петербургское отделение Математического института им. В. А. Стеклова Российской академии наук (saīsināti – ПОМИ РАН)) Sanktpēterburgā, Krievijā, Alfrēda Rēņi Matemātikas institūts (Rényi Alfréd Matematikai Kutatóintézet) Budapeštā, Ungārijā.
Aleksandrs Grotendīks (Alexander Grothendieck) ir saņēmis Fīldsa medaļu (Fields Medal) par fundamentāliem sasniegumiem algebriskajā ģeometrijā un homoloģiskajā algebrā, kā arī devis ieguldījumu kategoriju teorijā, attīstījis arī kūļu teoriju. Alēns Konnss (Alain Connes) ir ievērojams speciālists operatoru algebras un fon Neimana algebras teorijā, kurš par darbiem šajā jomā ir saņēmis Fīldsa medaļu. Aleksandrs Kurošs (Александр Геннадьевич Курош) ir strādājis abstraktajā algebrā, izveidojis pirmo moderno monogrāfiju par grupu teoriju, par savu darbību saņēmis Čebiševa prēmiju (Премия имени П. Л. Чебышёва). Anatolijs Maļcevs (Анатолий Иванович Мальцев) ir izveidojis tā dēvēto Sibīrijas skolu algebrā un matemātiskajā loģikā. Viņš ir viens no universālās algebras radītājiem, nozīmīgu rezultātu autors modeļu teorijā. Džons fon Neimans (Neumann János Lajos, vēlāk John von Neumann) ir izveidojis kvantu mehānikas, arī kvantu loģikas algebriskos pamatus, devis ieguldījumu operatoru teorijā un režģu teorijā. Amālija Emija Nētere (Amalie Emmy Noether) ir veikusi fundamentālus ieguldījumus gredzenu, lauku un algebru teoriju attīstībā, vispāratzīta par izcilāko sievieti matemātikas vēsturē. Bartels Lēnderts van der Vardens (Bartel Leendert Van der Waerden) ir izcils speciālists matemātikas vēsturē, strādājis arī grupu teorijā un algebriskajā ģeometrijā. Viņa 20. gs. trīsdesmitajos gados sarakstītā un dažādās valodās daudzkārt izdotā grāmata “Algebra” (Algebra) par mūsdienu algebru kļuva paraugs vēlākajām mācību grāmatām šajā jomā. Jefims Zeļmanovs (Ефим Исаакович Зельманов) ir saņēmis Fīldsa medaļu par ierobežotās Bernsaida problēmas atrisināšanu, kļuvis pazīstams arī neasociatīvo algebru un kombinatorisko grupu teorijā. Boriss Plotkins (Борис Исаакович Плоткин) ir ievērojams grupu teorijas speciālists, piecu monogrāfiju autors algebrā, radījis jaunu perspektīvu novirzienu algebriskajā ģeometrijā; Latvijas Universitātes goda doktors.
Jānis Cīrulis "Algebra". Nacionālā enciklopēdija. https://enciklopedija.lv/skirklis/-algebra (skatīts 26.02.2026)