Diskrēto matemātiku plašāk var raksturot kā matemātikas daļu, kas iekļauj visas tās matemātikas nozares, kuras pētī diskrētas matemātiskas struktūras: galīgas grupas, grafus, automātus, tekstus galīgā alfabētā, izlases no galīgas kopas, polinomus ar veseliem koeficientiem, naturālu skaitļu funkcijas un citas. Tā nodarbojas arī ar tādām pētāmo struktūru, to komponenšu un elementu kopām, kuru objektus – līdzīgi naturāliem skaitļiem – iespējams izkārtot galīgā vai bezgalīgā virknē, un ar dažāda veida sakarībām starp šiem objektiem. Diskrētus objektus aprakstošie lielumi var pieņemt tikai izolētas, citu no citas atdalītas vērtības. Visbiežāk tās ir veseli (retāk – racionāli) skaitļi pretstatā nepārtrauktiem lielumiem (tiem vērtības ir reāli skaitļi), kas raksturīgi dabaszinātnēs un daudzviet tehnikā, tāpēc arī matemātiskajā analīzē un radniecīgās nozarēs, respektīvi, nepārtrauktajā matemātikā. Īpaši nošķir tā dēvēto galīgo matemātiku – to diskrētās matemātikas daļu, kas interesējas tikai par galīgām struktūrām. Lieto arī nosaukumu “diskrētā analīze” ar neviennozīmīgu saturu. Bieži ar to saprot to pašu galīgo matemātiku, citkārt, piemēram, analītisko metožu lietojumus diskrētā matemātikā, bet pastāv arī tradīcija tā saukt tikai galīgos diferenču rēķinus. Plašākā nozīmē diskrētajai matemātikai dažkārt pieskaita visas tās matemātikas nozares (pat ja tajās aplūko ne tikai diskrētas struktūras), kurās nav principiālas nozīmes robežpārejas procesiem un nepārtrauktības idejai, piemēram, algebru, vispārējo kopu teoriju, elementāro ģeometriju. Matemātikas dalījums nepārtrauktajā un diskrētajā tomēr ir nosacīts. Ir metodes, kas kopīgas abām, piemēram, lineārās algebras, kombinatorikas vai asimptotiskās metodes. Ir matemātikas nozares, kurās atsevišķi jautājumi pieder vienai, citi – otrai matemātikas daļai (varbūtību, spēļu, dinamisko sistēmu teorijas, lineārā programmēšana). Nereti pat vienam matemātiskajam modelim ir gan diskrētas, gan nepārtrauktas komponentes vai īpašības (izsvērti grafi, matricas).
diskrētā matemātika
Saistītie šķirkļi
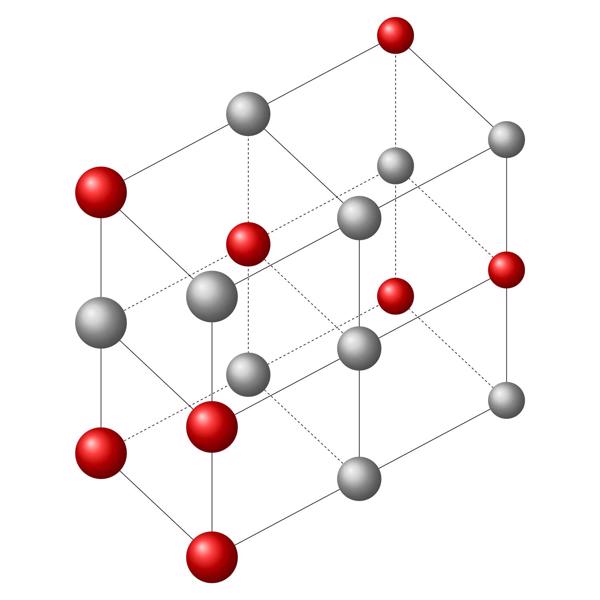
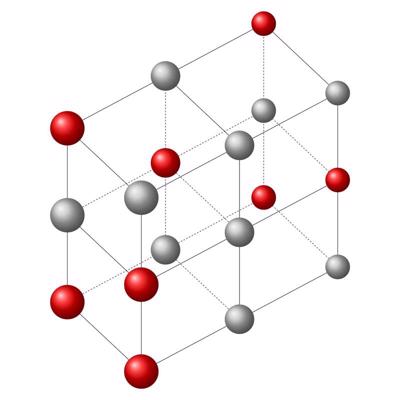
Diskrēta sistēma, ko veido savstarpēji saistīti objekti.
Pazīstamākās diskrētās matemātikas nozares ir algoritmu teorija, automātu teorija, diskrētā optimizācija, formālās valodas, funkcionālo sistēmu teorija, galīgo algebru (tostarp tā dēvētā daudzvērtību loģika) teorija, galīgo diferenču rēķini, grafu teorija, kodēšanas teorija, kombinatorika (ieskaitot diskrēto varbūtību teoriju), kriptoloģija, skaitļu teorija, veselo skaitļu aritmētika. Pie diskrētās matemātikas pieder arī atsevišķi algebras, matemātiskās loģikas, informācijas teorijas, skaitļu teorijas, spēļu teorijas un dažu citu nozaru jautājumi.
Mūsdienās jau ilgstoši galvenās diskrētās matemātikas teoriju rezultātu un metožu izmantotājas un tās attīstības veicinātājas ir datorzinātnes un ar to saistītās informācijas tehnoloģiju un telekomunikāciju nozares. No otras puses, diskrētā matemātika lielā mērā nodrošina to matemātiskos pamatus; tādas nozares kā algoritmu, automātu, grafu un informācijas teorijas, arī kodēšana bieži tiek pieskaitītas teorētiskajām datorzinātnēm. Diskrētajai matemātikai ir jauni lietojumi arī matemātiskajā bioloģijā un bioinformātikā, matemātiskajā lingvistikā, mākslīgā intelekta jomā un citur. Nozīmīgi, ka diskrētajā matemātikā izdevies radīt daudzu nepārtrauktās matemātikas jēdzienu un metožu diskrētos analogus, tā apejot nepieciešamību balstīties uz nepārtrauktību. Piemēram, ekstrēmu uzdevumos vairs nav nepieciešams, lai funkcija, kurai meklē ekstremālu vērtību, būtu nepārtraukta, un var izmantot paņēmienus, kas nepazīstami nepārtrauktajai matemātikai. Tas dod arī iespēju ar vienkāršākām diskrētām metodēm atrast tuvinātus atrisinājumus nepārtrauktās matemātikas uzdevumiem.

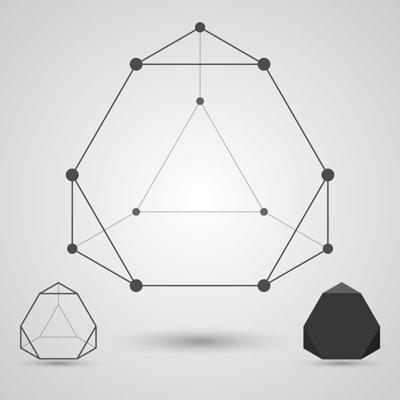
Grafu teorija ir ciešā saskarē ar grupu teoriju. Šis nošķelta tetraedra grafs ir saistīts ar alternējošo grupu A4.
Diskrētajā matemātikā risināmo uzdevumu – gan teorētisko, gan praktisko – raksturīgākie tipi ir šādi: 1. - eksistences uzdevumi – vai noteikta veida objekti eksistē. Šādi uzdevumi ir ikvienā matemātikas nozarē; diskrētajā matemātikā tie bieži ir konstruēšanas uzdevumi: vai un kā var izveidot konkrētu vajadzīgā veida objekta, piemēram, diskrētas sistēmas, piemēru. Radniecīgas eksistences uzdevumiem ir tā dēvētās masu problēmas, kur bezgalīgam skaitam atsevišķu, bet līdzīgu uzdevumu jāatrod kopīgs, vienots risināšanas algoritms, kas katram uzdevumam dod kādu atrisinājumu (vai visus) vai arī pasaka, ka atrisinājuma nav; 2. - skaitīšanas uzdevumi – vai ir galīgs skaits noteikta veida objektu un cik tas liels. Dažkārt pietiek vai izdodas precīza skaita vietā atrast tam tikai kādu augšēju vai apakšēju novērtējumu. Kad skaitāmo objektu ir neierobežoti daudz, tos dažkārt sadala grupās pēc to sarežģītības (kas atsevišķam objektam vienmēr ir ierobežota un raksturojama ar vienu vai vairākiem naturāliem skaitļiem, piemēram, virsotņu un šķautņu skaits grafā, iekšējo stāvokļu skaits galīgā automātā) un skaitīt, cik ir vienādas sarežģītības objektu (to skaits vienmēr ir galīgs); 3. - novērtēšanas uzdevumi – kādās robežās mainās kāds noteikta veida objektu raksturlielums. Vērtējamajam lielumam var būt visiem objektiem derīga augšējā vai apakšējā robeža, bet biežāk tā vērtība izrādās atkarīga no objekta sarežģītības; tad meklē asimptotiskus novērtējumus, kas rāda, kā raksturlieluma vērtība aug līdz ar objekta sarežģītību; 4. - optimizācijas jeb ekstrēma uzdevumi – vai starp noteikta veida objektiem pastāv kāds zināmā nozīmē vislabākais vai vismaz kāds pietiekami labs; atrast tādu. Vairāku ekstrēmu uzdevumos izvērtēšana jāveic pēc vairākiem kritērijiem; 5. - atlasīšanas uzdevumi – starp visiem noteikta veida objektiem atrast tos, kam piemīt viena vai vairākas īpašas pazīmes, vai noskaidrot tikai to skaitu kā otrajā punktā minētajā gadījumā.
Netriviālos gadījumos nepieciešams pārskaitošs algoritms, kas spēj visus vajadzīgos objektus (to aprakstus, konstrukcijas priekšrakstus vai tml.) tādā vai citādā secībā pa vienam ģenerēt. Kad objekti ir veseli skaitļi, bieži šim nolūkam izmanto rekursīvas virknes. Saprotams, ka, ja apskatāmo objektu (vispārīgāk – iespējamo variantu) ir galīgs skaits, tad ceturtā un piektā tipa uzdevumi principā ir atrisināmi, izmantojot objektu tā dēvēto pilno pārlasi, taču tīrā veidā šāda metode parasti ir darbietilpīga un tāpēc neefektīva.
Svarīgi ir arī masu problēmu atrisināmības un esošo algoritmu sarežģītības novērtējumi, kā arī vienkāršāku algoritmu meklēšana tādām masu problēmām, kuru risināšanai algoritmi jau zināmi. Risinājumu pamatošanai (un vispār dažādu apgalvojumu pierādīšanai vai pārbaudei) izmanto labi zināmo matemātisko indukciju un tās vispārinājumu – dažādas rekursijas metodes, kas gan nav piemērotas visos gadījumos. Plaši izmanto arī dažādas algebriskas metodes.
Savos iesākumos, kad bija pazīstami tikai pozitīvie veselie skaitļi, matemātika bija diskrēta. Piemēram, Ēģiptē jau Vidējās valsts laikā (pirms 16. gs. p. m. ē.) un arī vēlāk nodarbojās ar naturālo skaitļu saskaitīšanas un sareizināšanas metodēm. Pēc tam skaitļu teorijas elementi atrodami arī sengrieķu zinātnieku Pitagora (Πυθαγόρας) (Pitagora trijstūri), Erastotena (Eρατοσθένης) (“Erastotena siets” pirmskaitļu nošķiršanai) un Diofanta (Διόφαντος) darbos (tā dēvētie Diofanta vienādojumi un to risināšana). Tomēr senatnē matemātiķu intereses diskrētās matemātikas jomā bija saistītas galvenokārt ar kombinatoriku. Pēc senās Grieķijas perioda kombinatorika veidojās un attīstījās ārpus Eiropas. Piemēram, 9. gs. vidū Indijā bija zināmas formulas permutāciju un kombināciju skaita aprēķināšanai, bet Ķīnā un islāma zemēs pazina binomiālo koeficientu īpašības. Renesanse atdzīvināja kombinatoriku arī Eiropā. Tās attīstību, tostarp diskrētās varbūtību teorijas izveidošanos, veicināja vēlme matemātiski izprast dažādas spēles. Pateicoties 17. gs. franču matemātiķim Blēzam Paskālam (Blaise Pascal) un vācu matemātiķim Jākobam Bernulli (Jakob Bernoulli), bet īpaši 18. gs. šveiciešu matemātiķim Leonardam Eileram (Leonhard Euler), kombinatorika kļuva par patstāvīgu matemātikas nozari ar savu teorētisko bāzi. Tā kopš 1718. gada ir pazīstams kombinatorikai nozīmīgais ieslēgšanas un izslēgšanas princips. Būtībā gan kombinatorikai, gan grafu teorijai pieder jau 9. gs. pazīstamā šaha zirdziņa problēma (kā zirdziņam apiet šaha galdiņu, katrā lauciņā esot vienu reizi). Atsevišķi uzdevumi un problēmas, ko var atzīt par grafu teorijai piederīgiem, matemātiķiem bija pazīstami arī vēlāk, piemēram, 18. gs., kad Kēnigsbergā populārs uzdevums bija visu septiņu tiltu apiešana, pa katru ejot vienu reizi. L. Eilera 1736. gada publikācija par to, kāpēc tiltus tā apiet nav iespējams, kļuva par pamatu vēlākajai grafu teorijas sadaļai par Eilera ķēdēm un cikliem un tiek uzskatīta par pirmo publikāciju grafu teorijā. Četru krāsu problēma (vai iespējams katru karti izkrāsot ar četrām krāsām, kaimiņvalstis iekrāsojot atšķirīgi), kas formulēta 1852. gadā, ir cits pazīstams grafu teorijas uzdevums, kas pozitīvi tika atrisināts tikai 1976. gadā – šis rezultāts kļuva par pirmo matemātikas teorēmu, kas pierādīta, izmantojot datoru. 1857. gadā parādījās pirmie raksti par tādu tagad populāru diskrētu struktūru kā koki. Vienlaikus ar grafu teoriju 19. gs. beigās izveidojās vai sāka veidoties arī vairākas citas teorijas, kas pašlaik pilnībā vai daļēji ir diskrētās matemātikas sastāvā, piemēram, galīgās un vispārīgāk – diskrētās ģeometrijas, Būla algebras, kopu algebra, algebriskā kombinatorika, kas saistītas ar tādiem zinātniekiem kā Džordžs Būls (George Boole), Arturs Keilijs (Arthur Cayley), Persijs Aleksandrs Makmahons (Percy Alexander MacMahon), Džeimss Džozefs Silvestrs (James Joseph Sylvester) un citi. Diskrētā matemātika ievērojami paplašinājās 20. gs., rodoties daudzvērtību loģikām (20. gados), precīzam algoritma jēdzienam algoritmu teorijai (30.–50. gados), daudzvērtību loģiku un funkcionālo sistēmu teorijām (20. gados), automātu teorijai (50. gados), kriptogrāfijai un kodēšanas teorijai, kurām gan ir jau gadsimtus ilga priekšvēsture (50.–60. gados) un citām. Vairākas tai piederīgas matemātikas nozares 20. gs. otrajā pusē piedzīvoja strauju attīstību (kā automātu teorija, grafu teorija, formālās gramatikas) vai ir radušās no jauna (kā datorģeometrija, datorgrafika), jo parādījās elektroniskās skaitļošanas mašīnas jeb datori, tīmeklis, attīstījās informācijas tehnoloģijas. Tam visam bija vajadzīga teorētiska, tostarp matemātiska, bāze. Ar algoritmu teoriju jēdzieniski saistītais naturālo skaitļu funkciju izrēķināmības jēdziens tiek atzīts par vienu no nozīmīgākajiem visā diskrētajā matemātikā. Bet kopš astoņdesmitajiem gadiem augstskolu mācību plānos (vispirms Amerikas Savienotajās Valstīs (ASV), tad arī Eiropā un citur) sāka parādīties dažāda satura diskrētās matemātikas kursi.

Blēzs Paskāls.

Jākobs Bernulli.

Leonards Eilers.
Viena no septiņām tā dēvētajām “tūkstošgades problēmām” matemātikā ir algoritmu teorijas labi zināmā un nozīmīgā P = NP problēma, kas neformālā izklāstā nozīmē jautājumu, vai taisnība, ka, ja kāds uzdevums principā nav viegli atrisināms, tad nevar būt viegli arī tā atrisinājumu pārbaudīt. Pozitīva atbilde uz šo jautājumu nozīmētu, ka daudzu veidu sarežģītus uzdevumus ir iespējams atrisināt vienkāršāk, nekā to spēj izdarīt pašlaik. Praktiskā aspektā un arī pētījumos arvien nozīmīgāki kļūst diskrētās optimizācijas un vairāku ekstrēmu uzdevumi un to risināšanas metodes, arī algoritmu sarežģītības jautājumi un dažu diskrētu struktūru, piemēram, grafu sarežģītības novērtējumi. Panākts zināms progress lielu grafu zīmēšanā (t. i., pārskatāmu to zīmējumu iegūšanā ar datoru).
Nozīmīgākie periodiskie izdevumi – Discrete Applied Mathematics (kopš 1979. gada; Elsevier (Nort Holland)); Discrete Mathematics (kopš 1971. gada; Elsevier (Nort Holland)); Discrete Mathematics, Algorithms and Applications (kopš 2009. gada; World Scientific); Discrete Mathematics and Applications (kopš 1989. gada; De Gruyter); SIAM Journal on Discrete Mathematics (kopš 1988. gada; Society for Industrial and Applied Mathematics); Дискретная математика (kopš 1989. gada; Математический институт им. В. А. Стеклова Российской академии наук).
Starp pazīstamākajām pētniecības iestādēm diskrētajā matemātikā ir Diskrētās matemātikas un teorētisko datorzinātņu centrs (Center for Discrete Mathematics and Theoretical Computer Science (DIMACS)) Pisketevejā, ASV; Grācas tehnoloģiju universitātes Diskrētās matemātikas institūts (Institut für Diskrete Mathematik, Technische Universität Graz) Austrijā; Krievijas Zinātņu akadēmijas V. A. Steklova Matemātikas institūts (Математический институт им. В. А. Стеклова Российской академии наук (МИАН)) Maskavā, Krievijā; Kloda Šenona institūts (Claude Shannon institute) Dublinā, Īrijā; Teorētisko datorzinātņu institūta Algoritmu, diskrētās matemātikas un optimizācijas centrs (Center for Algorithms, Discrete Mathematics and Optimization at the Institute of Theoretical Computer Science (CADMO)) Cīrihē, Šveicē.
Ungāru matemātiķis Pāls Erdēšs (Erdös Pál) ir darbojies dažādās diskrētās matemātikas nozarēs. Viņš ir atrisinājis un arī pats izvirzījis daudzas 20. gs. plaši apspriestas diskrētās matemātikas problēmas; ap 1500 matemātisku publikāciju autors. Ronalds Greiems (Ronald Lewis Graham), viens no diskrētās matemātikas attīstītājiem 20. gs. otrajā pusē, devis īpašu ieguldījumu Ramseja teorijā, ir vairāku monogrāfiju autors vai līdzautors, par savu darbu saņēmis dažādus apbalvojumus, kā, piemēram, Poja balva (Pólya Prize), Lestera R. Forda apbalvojums (Lester R. Ford Award) un Eilera medaļa (Euler Medal). Sergejs Jablonskis (Сергей Всеволодович Яблонский) ir viens no pazīstamās padomju Krievijas matemātiskās kibernētikas skolas pamatlicējiem, vairāku monogrāfiju un mācību grāmatu autors, veicis nozīmīgus atklājumus vadības sistēmu teorijā (теория систем управления), saņēmis vairākus tādus valdības apbalvojumus kā Ļeņina prēmija (Ленинская премия) un Darba Sarkanā karoga ordenis (Орден Трудового Красного Знамени). Donalds Knuts (Donald Ervin Knuth) devis lielu ieguldījumu algoritmu sarežģītības teorijā, ir autors daudzsējumu monogrāfijai “Programmēšanas māksla” (The Art of Computer Programming), kur lielākā daļa rakstu veltīti algoritmu teorijai un kombinatorikai; par savu darbu saņēmis vairākus profesionālos apbalvojumus, kā Tjūringa balvu (Turing Award), Nacionālo zinātnes medaļu (National Medal of Science). Klods Šenons (Claude Elwood Shannon), modernās informācijas teorijas un kriptogrāfijas pamatlicējs, devis ieguldījumu arī automātu teorijas un spēļu teorijas attīstībā, ap desmit pasaules universitāšu goda doktors, dažādu profesionālo apbalvojumu laureāts. Alens Tjūrings (Alan Mathison Turing) ir viens no algoritmu teorijas un teorētisko datorzinātņu radītājiem. Viņa vārdā par Tjūringa mašīnu nosauktais algoritmu paveids tiek uzskatīts par mūsdienu skaitļošanas mašīnu jeb datoru pirmo matemātisko modeli un idejisko priekšteci; arī vairāki citi diskrētās matemātikas jēdzieni ir saistīti ar viņa vārdu.
Jānis Cīrulis "Diskrētā matemātika". Nacionālā enciklopēdija. https://enciklopedija.lv/skirklis/-diskr%C4%93t%C4%81-matem%C4%81tika (skatīts 26.02.2026)