Kombinatorikai (dēvētai arī par kombinatorisko analīzi vai kombinatorisko teoriju) nav vispārpieņemtas definīcijas un nav arī striktu robežu. Tiek pat uzskatīts, ka nav iespējama tās viennozīmīga definīcija; tāda nav arī iepriekš formulētā. Bieži ar kombinatoriku tiek saprasta tikai t. s. skaitošā jeb enumeratīvā kombinatorika (vidusskolas programmās pat tikai tās elementārākā daļa). No otras puses, pastāv arī uzskats, ka būtībā kombinatorika ir dažādu disciplīnu apvienojums, taču nav vienprātības par to, kas šajā apvienojumā iekļaujams un kas ne, tāpat arī – vai kombinatorika neietver visu galīgo matemātiku. Tas daļēji skaidrojams ar dažādām tradīcijām un vajadzībām, bet laika gaitā mainās domas arī par to, ko īsti uzskatīt par kombinatorikas pamatobjektiem – konfigurācijām.

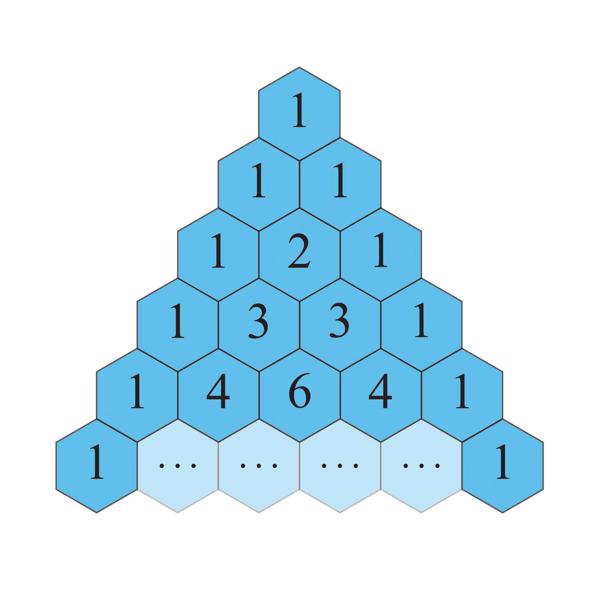
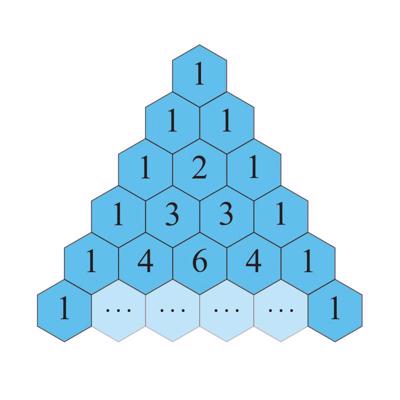
Tiek pieņemts, ka vispārīga konfigurācija (saka arī savienojums) kombinatorikā ir tāds veidojums no kādu kopu elementiem un apakškopām, kas pakļaujas norādītām likumībām vai kas izveidots, ievērojot norādītās prasības. Viena veida konfigurācijas ir tās, kam šie ierobežojumi ir vieni un tie paši. Dažkārt (atsevišķās apakšnozarēs) konfigurācijas saprot šaurāk – kā vienkāršas vai kādas īpašas uzbūves veidojumus. Vienkāršākās un visplašāk pazīstamās konfigurācijas ir t. s. izlases (izlase, kombinatorikā) – kombinācijas, variācijas un permutācijas, bet konfigurācija var būt arī sarežģīts hierarhisks veidojums.

Kombinatorikai raksturīgi uzdevumi ieņem vairāk vai mazāk nozīmīgu vietu ne vienā vien matemātikas nozarē un arī ārpus tās. Tas dod zināmu pamatu šādu nozari vai atbilstošu tās sadaļu pieskaitīt kombinatorikai, lai gan nav vienotu kritēriju, kuros gadījumos to darīt, kuros ne. No otras puses, atsevišķas kombinatorikas nodaļas piedzīvojušas strauju attīstību un izaugušas, tāpēc kādas no tām var tikt un nereti arī tiek uzskatītas par patstāvīgu diskrētās matemātikas sastāvdaļu. Kā piemēru tam var minēt grafu teoriju.

Kombinatorika ir līdzeklis diskrētu objektu veidošanas un struktūras likumību izzināšanai, modelējot tos šim nolūkam matemātiski. Kombinatorikai, arī grafu teorijai, ir lietojumi statistiskajā un kvantu fizikā, valodniecībā, grupu teorijā, ģeometrijā, molekulu struktūras pētījumos, ģenētikā, bet jo plaši datorzinātnē, arī sakaru un informācijas tehnoloģiju nozarēs. Tai ir lietojumi arī matemātikā, kur visdažādākajās apakšnozarēs sastopami diskrēti veidojumi. Daudzas kombinatorikas idejas un metodes tiek izmantotas arī bezgalīgām kopām kombinatoriskajā kopu teorijā; to dažkārt sauc arī par bezgalīgo kombinatoriku.

Matemātikas tematu klasifikācijas shēmā (Mathematics Subject Classification, MSC2010) uzrādītas piecas kombinatorikas apakšnozares, kuras tātad var uzskatīt par nozīmīgākajām: skaitošā kombinatorika, kombinacionālo shēmu un konfigurāciju teorija, grafu teorija, ekstremālā kombinatorika, algebriskā kombinatorika. Skaitošā kombinatorika ir senākā un pazīstamākā kombinatorikas daļa, savukārt grafu teorija ir tā, kura attīstās visstraujāk. Var minēt vēl citas pietiekami patstāvīgas kombinatorikas nodaļas: analītisko, aritmētisko (jeb skaitļu), ģeometrisko, topoloģisko, varbūtisko, vārdu kombinatoriku, sadalījumu teoriju, matroīdu teoriju un citas.

Tālāk minētie pieci principi ir t. s. kombinatorikas pamatprincipi, kaut gan pieder pie skaitošās kombinatorikas. Tiem ir arī vispārīgāki varianti.

Saskaitīšanas jeb summas princips: ja kādu izvēli α var izdarīt m dažādos veidos, bet izvēli β – n citos veidos, tad apvienoto izvēli α vai β var izdarīt m + n veidos.

Sareizināšanas jeb reizinājuma princips: ja kādu izvēli α var izdarīt m dažādos veidos un, neatkarīgi no tās iznākuma, izvēli β – n veidos, tad divkāršo izvēli α un β var izdarīt m × n veidos.

Vienlieluma princips: ja starp izvēles α iznākumiem un izvēles β iznākumiem pastāv kāda savstarpēji viennozīmīga atbilstība un izvēli α var izdarīt m veidos, tad arī izvēli β var izdarīt tikpat veidos.

Dirihlē (arī baložbūru) princips: ja skaitlis n ir sadalīts m saskaitāmajos, kur m < n (saskaitāmie drīkst būt vienādi), tad vismaz viens saskaitāmais ir lielāks par 1.

Ieslēgšanas un izslēgšanas princips (šeit trim kopām): pieņemot, ka elementu skaitu patvaļīgā kopā X apzīmē ar |X|, galīgām kopām A, B, C šis princips nosaka, ka

|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|,

t. i., ka to apvienojuma elementu skaitu iegūst, vispirms “ieslēdzot” tajā visu trīs kopu elementu skaitus, tad no jau iegūtā “izslēdzot” katram kopu pārim kopīgo elementu skaitus, un beidzot vēl “ieslēdzot” tām visām kopīgo elementu skaitu.

Simboliskā metode analītiskajā kombinatorikā nozīmē, ka starp kombinatorisku objektu klasēm pastāvošās sakarības (arī skaitliskās) īpašā veidā pārtulko atbilstošu veidotājfunkciju valodā, kuras pēc tam var pētīt ar matemātiskās analīzes metodēm, rezultātus interpretējot atkal kombinatoriski.

Pierādījumos plaši tiek izmantota labi zināmā matemātiskās indukcijas metode. Ir divas tipiskas kombinatoriska pierādījuma metodes. Bijekcijas metode balstās uz minēto vienlieluma principu, pēc kura pierādīt, ka divām kopām ir vienāds elementu skaits, to var izdarīt, nodibinot starp tām bijekciju – savstarpēji viennozīmīgu atbilstību. Divējādā skaitīšana ir metode kombinatorisku vienādību pamatošanai: ja izteiksmes vienādības abās pusēs izdodas interpretēt kā divus vienas un tās pašas kopas elementu skaita aprēķinus atbilstoši diviem dažādiem šo elementu skaitīšanas veidiem, tad šīm izteiksmēm vērtības ir vienādas. Arī t. s. varbūtību metode ir pierādīšanas metode, ko var lietot, kad jānoskaidro, vai kādā konfigurāciju klasē K ir konfigurācijas ar noteiktām īpašībām. Ja var parādīt, ka, izraugoties nejaušas konfigurācijas no K, varbūtība iegūt tādu, kam šīs īpašības piemīt, ir lielāka par 0, tad tas nozīmē, ka vismaz viena vajadzīgā konfigurācija eksistē.

Kombinatorika ir joma, kur teorēmu pierādīšanai iespējams izmantot arī datoru, kaut gan jautājums par tā iegūtā pierādījuma korektumu ir diskutabls.

Atsevišķi jēdzieni, paņēmieni un rezultāti, ko tagad uzskata par kombinatoriskiem, bija zināmi gan Senajā Ēģiptē un (mazāk) Grieķijā, gan Senajos Austrumos (Indijā un Ķīnā). Senākais zināmais kombinatorisku paņēmienu lietojums fiksēts jau 16. gs. p. m. ē. ēģiptiešu papirusā (par naturālu skaitļu sadalīšanu saskaitāmajos). Bija zināma Ņūtona binomiālā formula, kombināciju skaits, binomiālie koeficienti un to īpašības, tāpat pazīstami maģiskie kvadrāti, risināti atsevišķi konkrēti kombinatoriskie, jo īpaši dažādu konfigurāciju skaitīšanas uzdevumi.

Vēlāk, agrīnajos viduslaikos, tika izmantoti daži tagadējās grafu teorijas jēdzieni, bija sīki izpētītas dažādas situācijas, kurās parādās kombinācijas un variācijas; aizvien tika risināti dažādi kombinatoriski uzdevumi. Persiešu 11. un 12. gs. matemātiķis un inženieris Abū Bakrs Muhameds bin al Karadžī (Abū Bakr Muḥammad ibn al Ḥasan al-Karajī vai al-Karahī), domājams, pirmais pamatojis binomiālo formulu un Paskāla trijstūri. Tagad zudušā viņa darbā bijusi arī ievesta ideja pierādījumam ar matemātisko indukciju.

Eiropā kombinatoriku ieviesa 13. gs. no arābu valstīm un Indijas, pateicoties Leonardo Fibonači (Leonardo Fibbonacci) darbiem. Pat tikai no 16. gs. zināmi vēl atsevišķi izolēti eiropiešu pētījumi, bet plašāka kombinatorikas attīstība sākās 17. gs. Franču zinātnieks Blēzs Paskāls (Blaise Pascal), nodarbojoties ar binomiālajiem koeficientiem, izklāstīja un arī pamatoja to īpašības. Viņa un Pjēra Fermā (Pierre de Fermat) sarakstē par azarta spēlēm tika apspriesti ne vien varbūtību teorijas, bet arī vairāki netriviāli kombinatorikas jautājumi. B. Paskālu un Gotfrīdu Leibnicu (Gottfried Wilhelm von Leibniz, arī Leibnitz) uzskata par mūsdienu kombinatorikas aizsācējiem. 1666. gadā Leipcigā G. Leibnics izdeva savu paplašināto disertācijas darbu “Par kombinatorikas mākslu” (De arte combinatoria), kurā, domājams, pirmo reizi parādījies vārds “kombinatorika”. Tiesa gan, grāmatas autora ieskatā, tas aptvēra faktiski visu zināmo galīgo matemātiku un pat loģiku. 17. gs. sāka veidoties arī terminoloģija.

Kombinatorika kā patstāvīga matemātikas nozare galīgi noformējās 18. gs., pateicoties šveiciešu matemātiķa Leonarda Eilera (Leonhard Euler) ieguldījumam. Viņš pētījis latīņu kvadrātus, sadalījumus, arī kombinācijas un variācijas ar ierobežojumiem, permutāciju vispārinājumus, lietojis jaunas metodes, atrisinājis vairākus populārus kombinatoriskas dabas uzdevumus, uzrakstījis arī pirmo nopietno publikāciju grafu teorijā.

19. gs. aizsākās daudzi jauni kombinatorikas virzieni, piemēram, skaitošā (enumeratīvā) grafu teorija (Arturs Keilijs, arī Arturs Keli (Arthur Cayley)), blokshēmu teorija (Tomass Kērkmens (Thomas Penyngton Kirkman) un Jakobs Šteiners (Jakob Steiner)), sakārtotu kopu kombinatorika (Rihards Dedekinds (Julius Wilhelm Richard Dedekind)). Radās un kļuva pazīstamas daudzas problēmas, gan ļoti nopietnas (ievērojamākā bija t. s. četru krāsu problēma, ko atrisināja apmēram simt gadu vēlāk ar datora palīdzību), gan tādas, kas radušās no izklaides uzdevumiem.

20. gs. sākumā parādījās pirmās grāmatas jaunlaiku kombinatorikā. Strauji paplašinājās kombinatorikas sakari ar citām matemātikas un arī nematemātiskām nozarēm, kurās tika atklātas struktūras, ko var pētīt, un uzdevumi, ko var risināt ar kombinatorikas metodēm (izveidojās kombinatoriskā ģeometrija, spēļu teorija, optimizācijas teorija, ķīmija); jauna veida uzdevumu avots bija informācijas teorija. Arī otrādi – starp citu matemātikas nozaru raksturīgajām metodēm bija tādas, kas noder kombinatorikas problēmu risināšanā (radās vai attīstījās topoloģiskās, algebriskās, varbūtiskās kombinatorikas virzieni). Par kombinatorikas izaugsmi liecina specializētu žurnālu parādīšanās gadsimta otrajā pusē.

Kopš 20. gs. beigām, attīstoties datorzinātnei un informācijas tehnoloģijām, īpaši tīmeklim, aizvien noderīgāka šajās nozarēs kļūst diskrētā matemātika, arī kombinatorika un jo īpaši grafu teorija. Tas ne vien ietekmējis pētāmo struktūru izvēli, bet ir arī licis meklēt jaunas kombinatorikas metodes – gan teorijas, gan uzdevumu risināšanas vajadzībām.

Kombinatorikā allaž ir bijis jūtams kāda kopēja skatījuma trūkums uz tās daudzajām metodēm, problēmām, atradumiem, tāpat arī vienojošu saišu trūkums starp tās atsevišķām nodaļām. Kopš 20. gs. 60. gadiem tādas saites un vienojoši principi tiek meklēti un veidojas. Balstoties uz jaunām algebriskām struktūrām (piemēram, incidences algebras) un jaudīgām kombinatorisko identitāšu klasifikācijas metodēm (umbrālie rēķini u. c.), mūsdienu kombinatorika pamazām kļūst viengabalaināka.

Oksfordas Universitātes (University of Oxford) Matemātikas institūts (Mathematical Institute) Lielbritānijā; Sidnejas Universitātes (The University of Sydney) Matemātikas un statistikas skola (School of Mathematics and Statistics) Austrālijā; Mičiganas Tehniskās Universitātes (Matemātisko zinātņu nodaļas) Kombinatorikas pētījumu institūts (Michigan Technological University (Department of Mathematical Sciences) Combinatorics Research Institute) Amerikas Savienotajās Valstīs; Grācas Tehnoloģiju Universitātes (Technische Universität Graz) Diskrētās matemātikas institūts (Institut für Diskrete Mathematik) Austrijā; Vaterlo Universitātes (Waterloo University) Kombinatorikas un optimizācijas nodaļa (Department of Combinatorics and Optimization) Kanādā.

Ars Combinatoria (kopš 1976. gada; Charles Babbage Research Centre, Winnipeg); Combinatorica (kopš 1981. gada; János Bolyai Mathematical Society and Springer); Discrete Applied Mathematics (kopš 1979. gada; Elsevier (North-Holland)); Journal of Combinatorial Designs (kopš 1993. gada; Wiley); Journal of Combinatorial Optimization (kopš 1997. gada; Springer); Journal of Combinatorial Theory. Series A & Series B (kopš 1997. gada; Elsevier (Academic Press)); The Journal of Combinatorial Mathematics and Combinatorial Computing (kopš 1987. gada, Charles Babbage Research Centre, Winnipeg).

Klods Beržs (Claude Jacques Berge), franču matemātiķis, viens no modernās kombinatorikas, īpaši grafu teorijas, pamatlicējiem 20. gs. vidū, piecu monogrāfiju (trīs no tām par kombinatoriku un par grafu teoriju) autors. Izvirzījis divas (mūsdienās pierādītas) hipotēzes un formulējis vairākas svarīgas teorēmas, kas kopumā sekmēja kombinatorikas attīstību pagājušajā gadsimtā.

Dorons Ceilbergers (דורון ציילברגר; angliski Doron Zeilberger), ebreju matemātiķis, devis ieguldījumu vairākās kombinatorikas nodaļās, pierādījis dažas pazīstamas hipotēzes, saņēmis no Amerikas Matemātikas biedrības (American Mathematical Societ) Leroja Stīla balvu (Leroy P. Steele Prize) par publikāciju (kopā ar Herbertu Vilfu (Herbert Saul Wilf)) kombinatorisko identitāšu teorijā un Deivida Robinsa balvu (David P. Robbins Prize), bet starptautiskais Kombinatorikas un lietojumu institūts (Institute of Combinatorics and its Applications) Floridā viņam piešķīris arī Eilera medaļa (Euler Medal).

Pāls Erdēšs (Erdös Pál) izvirzījis vairākas hipotēzes grafu teorijā; daudzu publikāciju autors. Daudz darījis Ramseja teorijā, varbūtību teorijas metožu ieviesējs ekstremālajā kombinatorikā.

Herberts Raizers (Herbert John Ryser), amerikāņu matemātiķis, viens no ievērojamākajiem kombinatorikas pārstāvjiem 20. gs. Īpaši pieminams ieguldījums blokshēmu, kombinatoro funkciju, galīgu kopu sistēmu teorijā. Divu grāmatu autors par kombinatoriku. Bijis arī kombinatorikas un algebras žurnālu redkolēģiju loceklis.

Džans Karlo Rota (Gian-Carlo Rota), itāļu izcelsmes amerikāņu matemātiķis un filozofs, kas karjeras vēlīnā posmā pievērsies kombinatorikai. Strādājis ar incidences algebrām, ar dažādām īpašām virknēm, ielicis stingru pamatu t. s. umbrālajiem rēķiniem. Uzrakstījis ar līdzautoriem desmit darbu sēriju par kombinatorikas pamatiem, ar to kļūdams par vienu no modernās kombinatorikas pamatlicējiem 20. gs. Viņa vārdā sauc pazīstamu nevienādību, dažas hipotēzes, arī kādu algebrisku sistēmu.

H. Vilfs, amerikāņu matemātiķis, vairāku grāmatu autors. Par darbiem kombinatorikā saņēmis Eilera medaļu un kopā ar D. Ceilbergeru – Leroja Stīla balvu.