Universālā algebra pievēršas kopīgajam dažādās algebriskās sistēmās, arī līdzīgu algebrisku sistēmu klasēs, lieto tām visām kopīgus jēdzienus, pierāda apgalvojumus, kas ir spēkā daudzām sistēmām, respektīvi, to klasēm. Dažkārt gan šo un nosaukumu “vispārīgā algebra” lieto plašākā nozīmē, attiecinot to uz visu algebras apakšnozari, kuru pieņemts saukt par abstrakto jeb moderno algebru.
universālā algebra
Saistītie šķirkļi
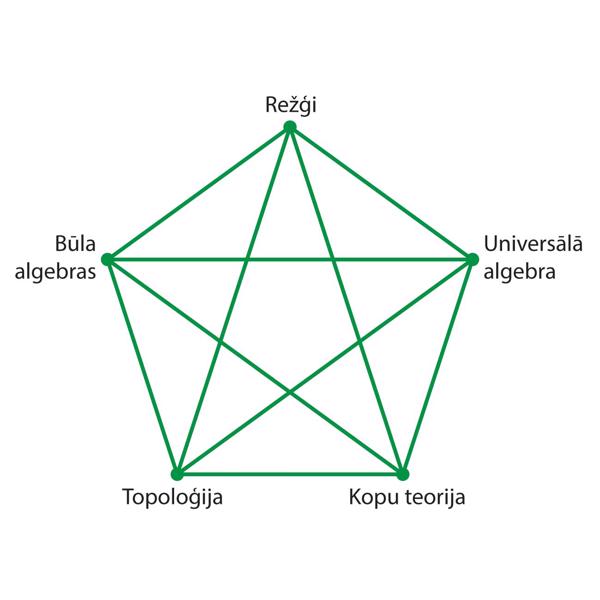
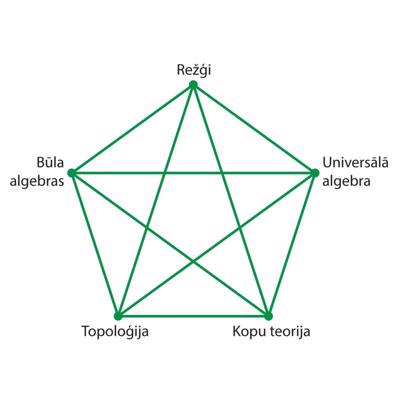
Universālā algebra un tās kaimiņnozares.
Algebriska sistēma ir sistēma, ko veido viena (parasti) vai vairākas kopas un izraudzītas darbības jeb operācijas ar to elementiem un/vai attiecības jeb relācijas starp tiem. Universālajā algebrā runā galvenokārt par vienas kopas algebriskajām sistēmām, kurās ir tikai operācijas; tā darīts arī turpinājumā. Šādas sistēmas sauc vienkārši par algebrām (savukārt sistēmas bez operācijām – par modeļiem). Parasti pieņem arī, ka algebra ir finitāra, t. i., ka katrai tās operācijai ir galīgs vietu skaits jeb aritāte, un daudzviet pietiek ierobežoties ar vienkāršāko gadījumu, kad arī operāciju skaits algebrā ir galīgs. Tad vispārīgā veidā kādu algebru 𝒜 pieraksta (𝐴, f1, f2, ..., f𝑘), kur 𝑘 > 0. Šeit A ir algebras pamatkopa, bet katrs simbols fi nozīmē vienu izraudzīto operāciju; tās sauc par algebras 𝒜 pamatoperācijām.
Divas algebras sauc par līdzīgām, ja tām ir vienāda garuma operāciju saraksti un ja operācijas ar vienu un to pašu kārtas numuru sarakstā ir arī ar vienādu vietu skaitu. Saka arī, ka tās ir viena tipa algebras: par algebras tipu sauc virkni (α) ≔ (α1, α2, …, αk), kur αi ir operācijas fi aritāte. Pieļauj arī 0-vietīgas operācijas. Tā vienveidības labad nosauc izraudzītus algebras elementus. Bieži viena otrai atbilstošajām līdzīgu algebru operācijām lieto arī vienu un to pašu apzīmējošo simbolu. Tad visu vajadzīgo operāciju simbolu kopu, kurā katram simbolam ir piesaistīts vietu skaits, sauc par atbilstošā tipa signatūru.
Vēl jāpiemin, ka dažās citās algebras nozarēs ar vārdu “algebra” saprot tikai kāda viena, šai nozarei vajadzīga veida algebras. Tad par iepriekš aprakstītajām vispārīga veida algebrām saka, ka tās ir universālas jeb vispārīgas algebras (ar nenoteikto galotni).
Universālā algebra interesējas arī par līdzīgu algebrisku sistēmu klasēm – to aksiomatizēšanu, struktūru, attiecībām starp dažādām vienas klases algebrām un arī par sakariem starp dažādām klasēm. Klase var saturēt visas viena tipa algebras vai arī tikai tās, kas apmierina noteiktas aksiomas, konstruētas ar kādu noteiktu paņēmienu vai kā citādi atlasītas.
Universālā algebra organizē ar algebriskām sistēmām saistītos jēdzienus un rezultātus vienotā un sistemātiskā kopumā, jo viens no tās uzdevumiem ir saskatīt, kur tas iespējams, kopīgo atšķirīgām sistēmām un arī sistēmu klasēm. Būdama vispārīga algebrisko sistēmu teorija, tā ir noderīga gadījumos, kad jāuzsāk kādas jaunas sistēmu klases pētīšana. Tā iezīmē pētījumu ietvaru, ļauj piemērot jau zināmas vispārējas teorēmas, saskatīt analoģijas citās sistēmu klasēs, dod piemērus un pretpiemērus. Tāpat universālās algebras pieredze noder, kad jāsalīdzina jau pazīstamas klases. Lietojumi ārpus algebras universālajai algebrai ir galvenokārt datorzinātnē, kur to izmanto, piemēram, abstrakto datu tipu teorijā, datubāzu teorijā, izkliedētās datošanas teorijā. Universālajai algebrai ir ciešs sakars arī ar mūsdienu matemātisko loģiku, kur tā palīdz gan loģisko sistēmu struktūras izpētē, gan to semantikas raksturošanā.
Matemātikas tematu klasifikācijā (angļu Mathematics Subject Classification; jaunākā versija MSC2020), ko izmanto matemātikas referatīvajos žurnālos, universālajai algebrai atvēlēta sadaļa “Vispārīgas algebriskas sistēmas (08)” (angļu General algebraic systems). Tajā ir trīs īpašas apakšsadaļas: A “Algebriskas struktūras” (angļu Algebraic structures), B “Varietātes” (angļu Varieties), C “Citas algebru klases” (angļu Other classes of algebras). Katra no tām sadalīta vēl sīkāk.

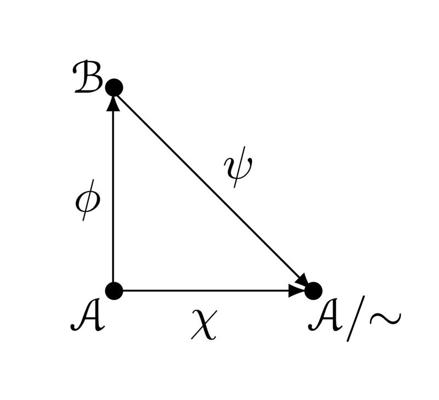
Homomorfismu teorēma: ja ϕ: 𝒜 → ℬ ir homomorfisms ar kodolkongruenci ∼ un ℬ = ϕ(𝒜), tad eksistē izomorfisms ψ: ℬ → 𝒜/∼, kuram kompozīcija ψϕ sakrīt ar dabisko homomorfismu χ: 𝒜 → 𝒜/∼.
Par algebras 𝒜 ≔ (𝐴, f1, f2, ..., fk) kongruenci sauc ekvivalences attiecību ∼ kopā A, kas ir stabila attiecībā pret visām algebras operācijām, t. i., katra operācija fi, kam katru argumentu aizstāj ar tam kongruentu, dod rezultātu, kas kongruents iepriekšējam: ja ∝1 ∼ β1, ∝2 ∼ β2, …, ∝m ∼ βm, tad fi(∝1, ∝2, …, ∝m) = fi(β1, β2, …, βm), kur m = αi. Ilustrācija: ja veselo skaitļu kopā ℤ nosacījums a ∼ b nozīmē, ka skaitļi a un b dod vienādu atlikumu, dalot ar 5, tad attiecība ∼ ir gredzena (ℤ, +, ×) kongruence. Piemēram, ja a1 ∼ b1, a2 ∼b2, tad arī (a1 + a2) ∼ (b1+ b2).
Pieņemam, ka dotas līdzīgas algebras 𝒜 = (𝐴, f1, f2, ..., f𝑘) un ℬ = (B, g1, g2, ..., g𝑘), kuru tips ir (∝1,∝2, …, ∝𝑘). Par algebras 𝒜 homomorfismu algebrā ℬ sauc tādu funkciju ϕ: A → B, ka ikvienai algebras 𝒜 operācijai fi
ϕ(fi(x1, x2, … xm)) = gi(ϕ(x1), ϕ(x2), …, ϕ(xm)),
kur m = ∝i. Homomorfismu ϕ sauc par izomorfismu, ja tas ir savstarpēji viennozīmīgs attēlojums (tad arī ϕ apgrieztā funkcija ir homomorfisms). Piemēram, apzīmējot visu pāra veselo skaitļu kopu ar 2ℤ, funkcija n ↦ 2n, kas katram veselam skaitlim piekārto tā reizinājumu ar 2, ir algebras (ℤ, +, 0) izomorfisms ar algebru (2ℤ, +, 0) un vienlaikus tās homomorfisms pašai sevī (epimorfisms), bet šī pati funkcija nav homomorfisms algebrā (ℤ, ×, 0).
Ja ϕ ir algebras 𝒜 homomorfisms, tad tā kodolekvivalence, proti, ekvivalence ∼ tās pamatkopā, ko definē ar a ∼ b :≡ ϕ(a) = ϕ(b), ir šīs algebras kongruence.
Tā ir tāda viena tipa algebru klase, kas satur tās un tikai tās šī tipa algebras, kas apmierina kādu noteiktu – galīgu vai bezgalīgu – vienādību sistēmu (aksiomas). Tādas ir daudzas nozīmīgas algebru klases, un tās arī ir vislabāk izpētītās. Ne katra aksiomatizēta klase ir ekvacionāla; piemēram, gredzeni signatūrā (+, ×) neveido ekvacionālu klasi, jo neitrālo elementu pretējā elementa eksistenci nevar aprakstīt ar vienādībām. Bet, apskatīti signatūrā (+, ×, --, 0, 1), tie veido (2, 2, 1, 0, 0) tipa ekvacionālu klasi.
Algebru ℬ = (B, g1, g2, ..., g𝑘) sauc par algebras 𝒜 ≔ (A, f1, f2, …, fk) apakšalgebru, ja A ir B apakškopa, kas noslēgta pret visām operācijām fi, un katra operācija gi ir attiecīgās operācijas fi sašaurinājums uz B (tad abām algebrām ir vienādi tipi).
Ja ϕ ir algebras 𝒜 homomorfisms kādā algebrā ℬ, tad kopas A attēls ϕ(A) ir B apakškopa, kas noslēgta pret visām algebras ℬ operācijām un tātad nosaka tās apakšalgebru, ϕ(𝒜). To sauc par algebras 𝒜 homomorfu attēlu.
Algebras 𝒜 ≔ (A, f1, f2, …, fk) faktoralgebra pēc kongruences ∼ ir algebra 𝒜/∼, kuras pamatkopa ir A faktorkopa A/∼ un i-ā operācija hj definēta ar hi([x1],[x2], ..., [xm]) = [fi(x1, x2, ..., xm)], kur [a] nozīmē elementa a kongruences klasi attiecībā uz ∼, bet m = αi. Attēlojums a ↦ [a] šeit ir homomorfisms 𝒜 → ℬ (t. s. dabiskais homomorfisms).
Par līdzīgu algebru saimes (𝒜j: j ∈ J) tiešo jeb Dekarta reizinājumu sauc tā paša tipa algebru ∏(𝒜 j: j ∈ J), kuras pamatkopa ir pamatkopu Aj Dekarta reizinājums, bet katra operācija definēta pa komponentēm. Divu algebru 𝒜 = (𝐴, f1, f2, ..., f𝑘) un ℬ = (B, g1, g2, ..., g𝑘) gadījumā tas nozīmē, ka 𝒞 ≔ (C, h1, h2, …, hk) ir šo algebru tiešais reizinājums 𝒜 x ℬ , ja C = A x B, bet katrai operācijai hi ar tipu m
hi((x1, x1), (x2, y2) …, (xm, ym)) = (fi(x1, x2, …, xm), gi(y1, y2, …, ym)).
Šeit attēlojums C → A, ko definē ar (a, b) ↦ a, ir homomorfisms 𝒞 → 𝒜. Līdzīgi ir ar attēlojumu (a, b) ↦ b.
Tā ir līdzīgu (viena tipa) algebru klase K, kas noslēgta attiecībā pret apakšalgebru, homomorfu attēlu un patvaļīgu tiešo reizinājumu veidošanu. Tas nozīmē, ka līdz ar katru savu algebru 𝒜 klase K satur visas 𝒜 apakšalgebras un visus tās homomorfos attēlus un ka jebkuras šīs klases algebru saimes tiešais reizinājums arī pieder K.
Viens no pirmajiem nozīmīgajiem universālās algebras rezultātiem bija t. s. Birkhofa teorēma par varietātēm: līdzīgu algebru klase ir varietāte tad un tikai tad, ja tā ir ekvacionāla, t. i., to var aksiomatizēt ar vienādībām. Vēlāk ir parādījušās vairākas līdzīgas teorēmas, kas sasaista klases aksiomu izskatu ar tās noslēgtību pret tām vai citām konstrukcijām.
Tā sauktā homomorfismu teorēma sasaista vairākus iepriekš aprakstītos jēdzienus, un tajā iesaistīti trīs dažādi homomorfismi. Formulējums: jebkurš algebras homomorfs attēls ir izomorfs tās faktoralgebrai pēc šī homomorfisma kodolkongruences.
Ir zināms, ka ikvienai algebrai visas apakšalgebras un visas kongruences veido pilnu režģi un ka patvaļīgs režģis ir izomorfs kādas algebras visu apakšalgebru režģim tad un tikai tad, ja tas izomorfs kādas – parasti citas – algebras visu kongruenču režģim. Visu algebras kongruenču režģim ir nozīmīga loma tās struktūras pētīšanā.
19. gs. beigās matemātikā jau bija pazīstamas pietiekami daudzas dažādas algebriskas sistēmas, lai būtu iespēja tās salīdzināt. Pirmoreiz tādu salīdzinājumu un vairākām sistēmām kopīgu iezīmju meklēšanu veica angļu matemātiķis, loģiķis un filozofs Alfreds Vaitheds (Alfred North Whitehead) 1898. gadā izdotajā grāmatā “Traktāts par universālo algebru” (A Treatise on Universal Algebra). Šajā darbā pirmoreiz parādījās nosaukums “universālā algebra”, un tas tika lietots ar nozīmi, kas ļoti līdzīga mūsdienu izpratnei. Ilgu laiku viņa darbam nebija īsta turpinājuma, līdz tikai nākamā gs. 30. gadu pašā sākumā parādījās Gereta Birkhofa (Garrett Birkhoff) un Eistena Ūres (Øystein Ore) publikācijas, kas pieskaitāmas universālajai algebrai. Piemēram, G. Birkhofs, veidojot režģu teoriju (angļu lattice theory), pamanīja tur virkni konstrukciju, kas radniecīgas dažās “klasiskajās” algebrās – grupu un gredzenu teorijās – jau lietotajām. Šis laiks arī tiek uzskatīts par universālās algebras sākumu. Turpmākās divās desmitgadēs liels skaits pētījumu abstraktajā algebrā notika G. Birkhofa aizsāktajā virzienā. Radās tādi nozīmīgi vispārīgi jēdzieni kā brīva algebra, apakšalgebru un kongruenču režģi, varietāte, algebru tiešais reizinājums. Tika atklāts, ka pastāv zināma dualitāte starp dažām svarīgām algebru klasēm un noteiktu topoloģisku struktūru klasēm – Stouna (pēc Māršala Stouna, Marshall Harvey Stone, vārda) dualitāte. Četrdesmitajos gados, mijiedarbojoties ar matemātisko loģiku, sāka veidoties modeļu teorija, radās interese ne vien par algebrām, bet arī par vispārīga veida algebriskām sistēmām. Ar tām nodarbojās Anatolijs Maļcevs (Анатолий Иванович Мальцев) un Alfreds Tarskis (Alfred Tarski). Brīvo algebru loma un nozīme pilnībā atklājās daudzās poļu algebras skolas piecdesmito gadu publikācijās, sākot ar Edvardu Marčevski (Edward Marczewski). Sešdesmitajos gados Viljams Lovers (William Lawvere) universālajā algebrā ieviesa kategoriju teorijas metodes. Sākot no sešdesmitiem gadiem, uzmanība tika pievērsta aksiomatizējamu algebru un algebrisku sistēmu klašu, īpaši kvazivarietāšu, teorijai. Tika arī pētīti apakšalgebru un kongruenču režģi (piemēram, Georgs Gretcers (angļu George Grätzer, ungāru Grätzer György)). Septiņdesmitajos gados universālās algebras attīstības līmeni apliecināja pirmās monogrāfijas (A. Maļcevs, Bjarni Jonsons (Bjarni Jónsson), Pauls Kons (Paul Moritz Cohn), G. Gretcers); tām ir nozīme arī mūsdienās. Īpašu uzmanību šai laikā pievērsa galīgām algebrām (Ralfs Makkenzijs, Ralph McKenzie); par patstāvīgu apakšnozari kļuva modeļu teorija. 20. gs. pēdējā ceturtdaļā, attīstoties datorzinātnēm, universālās algebras lietojumi tajās stimulēja pastiprinātu pievēršanos daudzsugu (angļu many-sorted) jeb heterogenām algebrām. Aktīvi attīstījās arī algebriskā loģika, kongruenčvarietāšu un dabiskās dualitātes (Čandlers Deiviss, Chandler Davis) teorijas.

Alfreds Vaitheds. Ap 1925. gadu.

Gerets Birkhofs. Ap 1950. gadu.
21. gs. universālo algebru joprojām izmanto datorzinātnē, kur tā dod dabisku algebrisku satvaru t. s. ierobežojumu apmierināšanas uzdevumiem (constraint satisfication problems), kas svarīgi mākslīgā intelekta laukā un arī programmēšanas teorijā.
Radusies t. s. universālā algebriskā ģeometrija (Boriss Plotkins, Борис Исаакович Плоткин), kas faktiski ir algebriskās ģeometrijas paplašinājums jebkādām algebriskām sistēmām.
Paplašinās vispārinātu algebrisku sistēmu, piemēram, t. s. daudzvērtīgo jeb hiperalgebru (algebru ar daudzvērtīgām operācijām) un nestrikto (angļu fuzzy) algebru, pētījumi. Regulāri tiek rīkotas starptautiskas konferences universālajā algebrā – bieži kopā ar citām saistītām algebras sadaļām, arī ar matemātisko loģiku.
Algebra Universalis (kopš 1971. gada; Springer)
Discussiones Mathematicae. General Algebra and Applications (kopš 2000. gada; University of Zielona Góra Press; De Gruyter)
Алгебра и логика (kopš 1962. gada; Сибирский фонд алгебры и логики)
Kolorado Universitātes Matemātikas nodaļa (Department of Mathematics, The University of Colorado) Boulderā, Amerikas Savienotajās Valstīs (ASV).
Krievijas Zinātņu akadēmijas Sibīrijas nodaļas S. L. Soboļeva Matemātikas institūts (Институт математики имени С. Л. Соболева Сибирского отделения Российской академии наук) Novosibirskā, Krievijā.
Lincas Universitātes Algebras institūts (Johannes Kepler Universität Linz, Institut für Algebra) Lincā, Austrijā.
Vanderbilta Universitātes Matemātikas nodaļa (Department of Mathematics, Vanderbilt University) Nešvilā, ASV.
Jānis Cīrulis "Universālā algebra". Nacionālā enciklopēdija. https://enciklopedija.lv/skirklis/-univers%C4%81l%C4%81-algebra (skatīts 26.02.2026)